xCanx
- 44
- 0
I have a problem, I did a motion lab in class and we had to observe a cart rolling down a ramp. We did it using the ticker tape. I calculated the average velocity and I got a graph like this.
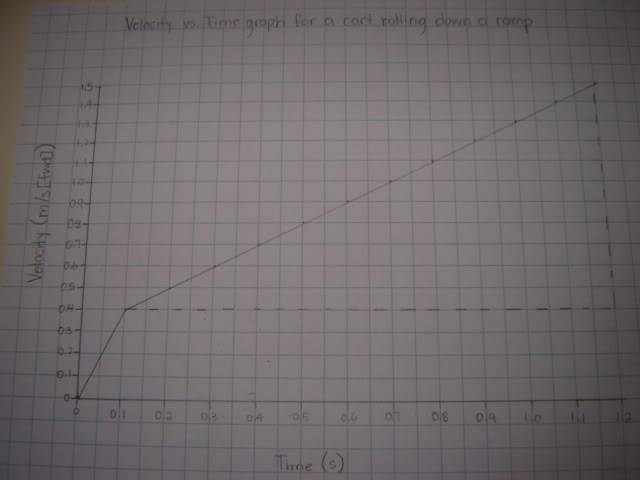
It's not straight, so I'm confused on how to calculate the acceleration and displacement using this velocity vs. time graph.
If you see that dotted line a drew, I was planning to use that slope for the accel. and the area under neath for displacement. Would this work?
I know there are errors, but I can't change the data.
It's not straight, so I'm confused on how to calculate the acceleration and displacement using this velocity vs. time graph.
If you see that dotted line a drew, I was planning to use that slope for the accel. and the area under neath for displacement. Would this work?
I know there are errors, but I can't change the data.