Sirsh
- 262
- 10
Hey all,
I've derived a fourth order dynamic system as represented by the following:
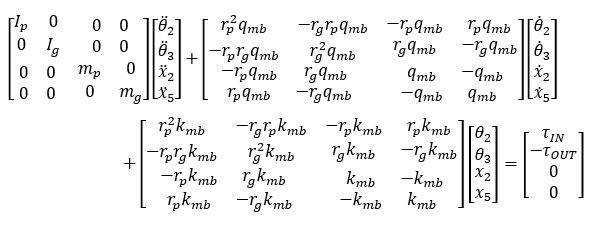
I need to determine the eigenvalues for this system to check whether they're purely real with no imaginary components.
How should I go about doing this? I have done eigenvalue problems in the past, but not to this extent. Would I just determine the eigenvalues for each matrix then do the addition of them?
Note: all the variables (excluding theta's and x's) have constant values.
Any help would be appreciated, thanks!
I've derived a fourth order dynamic system as represented by the following:
I need to determine the eigenvalues for this system to check whether they're purely real with no imaginary components.
How should I go about doing this? I have done eigenvalue problems in the past, but not to this extent. Would I just determine the eigenvalues for each matrix then do the addition of them?
Note: all the variables (excluding theta's and x's) have constant values.
Any help would be appreciated, thanks!