skybox
- 37
- 0
Hi all,
I am having an issue with the following problem. I just don't know how to approach it.
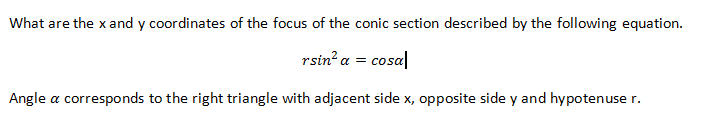
Ax^2 + Bxy + Cy2 + Dx + Ey + F = 0
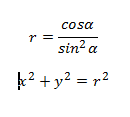
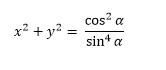
I am confused on how to put this problem in terms of x & y and get numerical values for both x & y. Any guidance would be greatly appreciated :)
I am having an issue with the following problem. I just don't know how to approach it.
Homework Statement
Homework Equations
Ax^2 + Bxy + Cy2 + Dx + Ey + F = 0
The Attempt at a Solution
I am confused on how to put this problem in terms of x & y and get numerical values for both x & y. Any guidance would be greatly appreciated :)