nvn said:
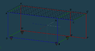
There is no wheel at point E', according to post 3. That wheel is instead located at point F.
There's also no point F ;) Let's see: the relevant part of post #3 was:
engineer356 said:
There will be a total of four supports on the corners of the entire box so there wont be one on the bottom where the beam meets 3/4 through the 50" beam.
... Ahhh ... I confused "won't" and "entire box" huh?
No worries - easy enough to shift the cone :)
I agree there is not enough information to solve for the reaction forces just yet ... and it is not best resolved as a statics problem.
We know:
I have a moment on the top right beam (390600 lb/in) and a distributed load of 160 lb/in
... this suggests a uniform load of 160lbs/in between AA' and BB' - it's com is right above the center of the box (being the volume ABED to A'B'E'D') ... so that won't destabilize the cart by itself.
The moment is problematic - the center of rotation is asserted to be CC' but I cannot think of a (sensible) way to build a cart so that will be the case ... what: is there a hinge there and something is pulling upwards from the other end of the cart? - anyway, the units are wrong.
I'd want to know where the moment comes from in more detail.
The moment comes from ... another beam attached on [CC'] directly in the middle.
... see, that does not sound like something that produces a moment about CC'.
It sounds like a lever or an additional weight... either would more likely create a moment about the diagonal: EF' or something.
At face value:
160lbs/in x 38"= 6080lbs(force) ... which is 231040lbs-in moment about CC' ... not enough, by itself, to balance the given moment there (if we just take the units as a typo). The unbalanced moment looks like it will lift the cart off it's wheels, pivoting it about CC'.
Maybe I'm making a mistake and "the entire top of the box" means the whole 50" from AA' to CC'? That would make a bigger force closer to the pivot.
160lbs/in x 50" = 8000lbs ... which is 200000lbs-in moment. Not big enough either.
Supports would have to be placed to the right of F' to counter the unbalanced moment.
(Or tie down the other end or something.)
... and there is no mention of the weight of the cart itself.
Since the whole point is to size the proper supports, I suspect that OP has reason to believe that the frame will not lift off the ground like that: perhaps it has already been built and it is a matter of choosing wheels that are strong enough(?) ... we don't actually know.
Aside:
@engineer365: how to handle distributed loads (JIC):
https://ecourses.ou.edu/cgi-bin/ebook.cgi?doc=&topic=st&chap_sec=04.5&page=theory