kakaho345
- 5
- 0
- Homework Statement
- See below
- Relevant Equations
- See below
As in title:

Plugging in the definition is straight forward, I am too lazy to type, I will just quote the book Fetter 1971:
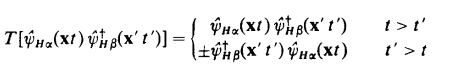
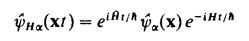
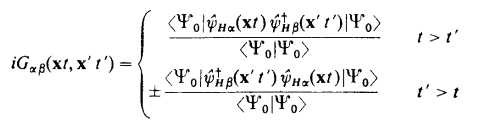
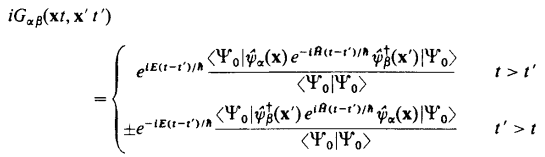
Up to here everything is very straight forward, in particular, since we are working on free electron gas, ##E=\hbar \omega##
However, I have no idea how to arrive here:
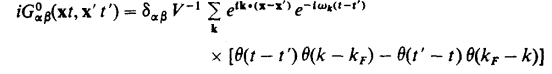
I understand that ##e^{ik\cdot(x-x')}## is from terms like ##\psi=e^{ikx}c##, however, the term ##e^{-i\omega_k(t-t')}## the sign doesn't look right to me for the two time region should have different signs in the exponential. Also, I don't know how to deal with the exponential sandwiched between the field operator. The step function in time is from the two pieces of time regions, but I am not sure on the step function in k. I may be from the filled Fermi sea.
I understand this is a very simple question. However, I have been sitting whole day dealing with this. Any help will be appreciated.
Plugging in the definition is straight forward, I am too lazy to type, I will just quote the book Fetter 1971:
Up to here everything is very straight forward, in particular, since we are working on free electron gas, ##E=\hbar \omega##
However, I have no idea how to arrive here:
I understand that ##e^{ik\cdot(x-x')}## is from terms like ##\psi=e^{ikx}c##, however, the term ##e^{-i\omega_k(t-t')}## the sign doesn't look right to me for the two time region should have different signs in the exponential. Also, I don't know how to deal with the exponential sandwiched between the field operator. The step function in time is from the two pieces of time regions, but I am not sure on the step function in k. I may be from the filled Fermi sea.
I understand this is a very simple question. However, I have been sitting whole day dealing with this. Any help will be appreciated.