Finding max speed and corresponding angle for a semi-circular path

[Juke]

Homework Statement

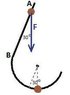
A model land-yacht runs on a horizontal frictionless oval track as shown (viewed
from above) in the figure. The curved parts of the track are semi-circles of radius
R = 0:5 m; the straight sides have length L = 1 m. The mass of the yacht (including
its sails) is m = 0:5 kg.

A child plays with the toy by starting the yacht from rest at point A at the beginning
of one of the straight segments of track (see diagram) and applying a force of mag-
nitude jFj = 4N to the sails, using a fan as shown. The force is horizontal, directed
at 30 (=6 radians) to the direction of the straight track (see diagram). Both the
magnitude and direction of the force remain constant throughout the game.

After passing B the yacht enters the curved section of the track on the right-hand
side of the diagram. Find the maximum speed reached by the yacht on this curved
section, and the angle (defined as shown) at which this maximum speed is attained.

http://img856.imageshack.us/img856/8205/40514750.jpg

Homework Equations

Derived equations of motion


F(centri) = mv^2/r

The Attempt at a Solution

I've tried resolving along a line parallel to the line L,
Fsin(theta) - 4cos30 = 0
and perpendicular
Fcos(theta) - 4sin30 = 0
(I assumed the acceleration was zero because of the direction I was resolving in was not along the line of the acceleration).

This had to be wrong as it just gave me theta = 30 and I also realized that the reaction force should have a role, but that would mean introducing an unknown force and angle which wouldn't allow me to find theta.

I've thought about using polar unit vectors and work-kinetic theorem but I'm still running into unknown values.

I'm a first year undergraduate.

First post, I apologise if I've broken any rules.

Thanks.

 

[TSny]

Hello, Juke. Welcome to PF!

I think the work-energy theorem is a good approach. Think about all the forces acting on the boat and which of those forces does work.

 

[Juke]

I've managed to figure out the angle to be 120 degrees. I just learned that the max speed occurs when the force F = 4N acts along the radius.

However I'm still stuck trying to find this speed. I've thought about which force does work, isn't it the force due to the fan? If I can remember correctly, the work done by a centripetal force is zero.

What I've tried is finding the horizontal distance moved from the point B to the point where theta is 120 degrees.
I got 1/2 * (1+cos30), I multiplied this by 4cos30. Then I equated this to 1/2 * m * (v^2 - u^2), with u^2 = 8root3

V = 5.18 m/s

 

[FireStorm000]

Your angle for theta is definitely correct; 120 degrees is the point where no force is acting parallel to the track. You need that in radians, which is 2∏/3

Your next step is to find the velocity entering the turn, which it sounds like you've already done.

After that, we have to find out how much velocity is gained in the turn. Because it's a friction-less track, and the path is already defined, you can basically forget restoring force: we know where the boat is going. If you know calculus, I'd set up and try to solve an integral ∫^2∏/3₀(F * sin(θ-∏/6))dθ

If you don't know calculus, this is much trickier, but let me know.

 

[TSny]

OK, good. Only the fan force does work. It does positive work until θ = 120^o, so that's the angle of max speed.

What I've tried is finding the horizontal distance moved from the point B to the point where theta is 120 degrees.
I got 1/2 * (1+cos30), I multiplied this by 4cos30. Then I equated this to 1/2 * m * (v^2 - u^2), with u^2 = 8root3

Check your calculation of the horizontal distance moved from point B. You will also need the work done for the vertical displacement moved from point B.

(Note: there is no need to break up the problem where you first find the speed at point B. You can set up work-energy between point A and the max speed point. But what you've done is ok.)

 

[Juke]

I know calculus but I don't know what steps you took to set up that integral.
I'm aware that the work done is the integral of the F(dot)dr.

What is F equal to in that integral?

 

[TSny]

You don't need to use calculus. For a constant force, the work is given by a dot product: $W = \textbf{F}\cdot \Delta \textbf{r}$ where $\Delta\textbf{r}$ is the overall displacement vector between initial and final points.

 

[Juke]

OK, good. Only the fan force does work. It does positive work until θ = 120^o, so that's the angle of max speed.



Check your calculation of the horizontal distance moved from point B. You will also need the work done for the vertical displacement moved from point B.

(Note: there is no need to break up the problem where you first find the speed at point B. You can set up work-energy between point A and the max speed point. But what you've done is ok.)

It should be 1/2 * (2 - cos30), I can see why is isn't what you highlighted.

Okay, so now the horizontal work done is [1/2 * (2 - cos30) x 4cos30], and the vertical
[1/2 *(1+sin30) x 4sin30]

Does it look right?

 

[TSny]

The horizontal displacement is still not correct. Your vertical displacement looks good!

 

[Juke]

The horizontal displacement is still not correct. Your vertical displacement looks good!

Oh I see, 'displacement'!, I worked out the distance.

So it should be just 1/2 * cos30.

 

[TSny]

Oh I see, 'displacement'!, I worked out the distance.

So it should be just 1/2 * cos30.

Right.

 

[Juke]

Now I got v = 5.08 m/s

 

[FireStorm000]

I know calculus but I don't know what steps you took to set up that integral.
I'm aware that the work done is the integral of the F(dot)dr.

What is F equal to in that integral?

Sorry, I wanted to make sure you knew calculus before I wrote a lengthy post. F would be the constant force, and the angle is between the track and the force. It would give you the energy gained in the curve. It's the first solution that came to mind for me.

You don't need to use calculus. For a constant force, the work is given by a dot product: W=F⋅Δr where Δr is the overall displacement vector between initial and final points.

True, but it doesn't mean you can't use calculus. Your way is probably simpler, the calculus approach is just what came to mind first.

 

[TSny]

Now I got v = 5.08 m/s

I think that's right. Good work.

For fun, you can compare this problem to another situation: Suppose you bent a wire into the shape of the track and placed the wire in a vertical plane as shown. Let a bead of mass .5 kg slide down the wire without friction and suppose the acceleration of gravity is 8 m/s² so that the force of gravity is 4 N. Find the position and value of the maximum speed of the bead.

 

[Juke]

Sorry, I wanted to make sure you knew calculus before I wrote a lengthy post. F would be the constant force, and the angle is between the track and the force. It would give you the energy gained in the curve. It's the first solution that came to mind for me.

Ill keep that in mind for when I do problems involving non constant forces.

Thanks

 

[Juke]

I think that's right. Good work.

For fun, you can compare this problem to another situation: Suppose you bent a wire into the shape of the track and placed the wire in a vertical plane as shown. Let a bead of mass .5 kg slide down the wire without friction and suppose the acceleration of gravity is 8 m/s² so that the force of gravity is 4 N. Find the position and value of the maximum speed of the bead.

You've been such great help, I really appreciate. The work-kinetic theorem makes more sense to me after working though this problem. I can't believe I've only just stumbled across this place, it's fantastic.

Ill attempt that problem in the morning, it's late where I am.

Thanks again.

 

[Dale4]

Just looking at this question, I still don't understand how the angle has been calculated. I understand it's necessary for there to be no net force perpendicular to the track, but lost after that.