smashX
- 12
- 0
Hi everyone. I've got a homework problem with Differential Calculus that drives me crazy for a couple of days so far and would like to ask you guys for a few suggestions
Given two parabolas, (C1): y = x2 and (C2): y = - (4-x)2. Find two points, each point on one parabola so that the distance between them is smallest.
The distance equation (I think)
Well, I called the point on (C1) (x1, y1), the other point (x2, y2). After that, I set up the distance equation and replace both y(s) with their respective x(s) as follow:
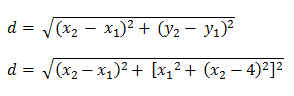
After that I got stuck ... since I don't know how to differentiate an equation with two variables. Here I need to find the minimum of d, which is the distance between the two points.
I wonder if my approach to the problem is wrong or what. Any suggestion is highly appreciated. Thank you.
And just a small question: I see lots of people type equations in our forum directly. Could you please show me how to do this? Every time I need to type a math formula, I have to open Word and it took me lots of time :( Thanks again.
Homework Statement
Given two parabolas, (C1): y = x2 and (C2): y = - (4-x)2. Find two points, each point on one parabola so that the distance between them is smallest.
Homework Equations
The distance equation (I think)
The Attempt at a Solution
Well, I called the point on (C1) (x1, y1), the other point (x2, y2). After that, I set up the distance equation and replace both y(s) with their respective x(s) as follow:
After that I got stuck ... since I don't know how to differentiate an equation with two variables. Here I need to find the minimum of d, which is the distance between the two points.
I wonder if my approach to the problem is wrong or what. Any suggestion is highly appreciated. Thank you.
And just a small question: I see lots of people type equations in our forum directly. Could you please show me how to do this? Every time I need to type a math formula, I have to open Word and it took me lots of time :( Thanks again.