Finding minterms from Multiplexer

[Blurpeys]

Homework Statement:

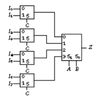
Determine the minterm list for Z(A,B,C,D) shown below. Assume the following values for the inputs: I(0)=0, I(1)=1, I(2)=D, I(3)=1⊕D, I(4)=0⊕D, I(5)=D⊕D, I(6)=1⊕0, I(7)=1⊕1. Also, assume that S(1) is the most significant select line for the 1-of-4 Mux.

Relevant Equations:

N/A

I(0)=0, so 0 and 1 are not minterms.
I(1)=1, so 2 and 3 are minterms.
I(2)=D, so 5 is a minterm but 4 is not a minterm.
I(3) not sure
I(4) not sure
I(5) not sure
I(6)=1⊕0=1, so 12 and 13 are also minterms.
I(7)=1⊕1=0, so 14 and 15 are not minterms.

I don't know how to deal with the rest of them, I am not even sure if the one I mentioned are correct.

 

[Baluncore]

Start by evaluating all the 8 input terms;
These three XOR terms could generate; 0, 1, D, or NOT(D)
I(3)=1⊕D ;
I(4)=0⊕D ;
I(5)=D⊕D ;