sodper
- 10
- 0
[SOLVED] Finding potential at certain points in circuit
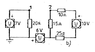
Calculate the potential of V_1 and V_2
See attached circuit configuration (circuit2.gif)
Ohms law: U = RI
Kirchhoff's laws
I tried to solve it with superposition but my teacher says I've got the wrong sign for V_2.
No matter how I try, I get a positive potential for V_2.
I've attached my solution (solution.jpg)
Any suggestions?
Homework Statement
Calculate the potential of V_1 and V_2
See attached circuit configuration (circuit2.gif)
Homework Equations
Ohms law: U = RI
Kirchhoff's laws
The Attempt at a Solution
I tried to solve it with superposition but my teacher says I've got the wrong sign for V_2.
No matter how I try, I get a positive potential for V_2.
I've attached my solution (solution.jpg)
Any suggestions?