385sk117
- 50
- 0
Homework Statement
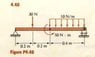
Find the reactions exerted on the members by the supports.
Homework Equations
Sigma Fx = Net force acting on x-axis = 0
Sigma Fy = Net force acting on y-axis = 0
Sigma M = Net Moments = 0
The Attempt at a Solution
10N/m -> changes to 4N at centre acting downward so total force acting downward is 34N
the Sum of two y component of two forces from suppors then equals to 34N
If I set the regarding point to be the point on the left supports, then total moment is
30 x 0.2 + 4 x 0.6 - 50 - Fy x 0.8 where Fy is the y component of force from the right support. But this gives negative value for Fy which means that the supporting force from the right side support is downward. How can this be true?
Any problem with my steps?
I neglected Fx as there is no movement of bar and only force acting in x direction is the x component of supporting from left support and that should be equals to 0
Attachments
Last edited: