Chandasouk
- 163
- 0
n the circuit shown in the figure find (a) the current in resistor R, (b) the resistance R, (c) the unknown emf, (d) f the circuit is broken at point x , what is the current in resistor R?
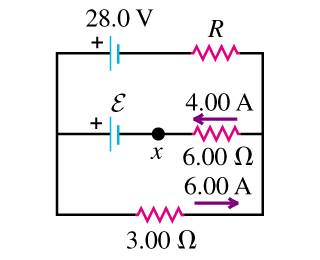
A) 2A using KCL
B)
C) 42V using KVL ofthe bottom loop
D)
For B, is the resistor 5 ohms? I'm not sure if I wrote my KVL correctly since the notation is different from my Electrical Engineering class but I wrote a KVL at the top loop, starting from the node to the left of the 28V voltage source, going clockwise so
-28-(-2A)R - 24V + 42V = 0
R = 5 ohms? I used -2A because I was going the opposite direction of the regular current.
That would mean for part D, the circuit simplifies to the loop of 28V-5 ohms-3ohms.
5 and 3 are in series so their equivalent resistance is 8. Then using V=IR, I is 28V/8 ohms
A) 2A using KCL
B)
C) 42V using KVL ofthe bottom loop
D)
For B, is the resistor 5 ohms? I'm not sure if I wrote my KVL correctly since the notation is different from my Electrical Engineering class but I wrote a KVL at the top loop, starting from the node to the left of the 28V voltage source, going clockwise so
-28-(-2A)R - 24V + 42V = 0
R = 5 ohms? I used -2A because I was going the opposite direction of the regular current.
That would mean for part D, the circuit simplifies to the loop of 28V-5 ohms-3ohms.
5 and 3 are in series so their equivalent resistance is 8. Then using V=IR, I is 28V/8 ohms