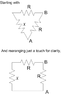Finding resistance of (semi-)infinite resistor chain between two points.

[physicsforus]

Homework Statement

What is the resistance of the (semi-)infinite resistor chain below, between points A and B, if R = 25 ohms?

The Attempt at a Solution

I am not sure where to begin exactly, but I am thinking of this formula:
VAB=VB-VA=∑ε-∑i.R
or
[PLAIN]https://www.physicsforums.com/latex_images/12/1284517-1.png

Just not quite for sure.

 

[collinsmark]

Hello physicsforus,

Welcome to Physics Forums!

I am not sure where to begin exactly, but I am thinking of this formula:
VAB=VB-VA=∑ε-∑i.R
or
[PLAIN]https://www.physicsforums.com/latex_images/12/1284517-1.png

Nah, the way to solve this is to start by actually finding some equivalent resistances.

I just solved this myself, and I admit its a bit tricky. There are a number of possible semi-infinite problems such as this, and I'll at least give you the strategy on how to solve this one, and then you can use the same strategy for other similar problems in the future.

Start with the right half of the figure, and draw a new resistor network with the 3 rightmost resistors, except, replace the 2R resistor with the variable 'x'. So in other words, you have 3 resistors, R, R, and x, all connected in series, and you're trying to find R_eq, as measured across one of the R resistors.

Why do we use the variable x? because at the moment, we don't know what left-looking equivalent resistance is at that node. Hypothetically, we could measure x by removing the two rightmost R resistors from the circuit, and place an Ohmmeter across x. That of course is assuming that we actually had such a circuit hooked up; but of course we don't, so we'll just call it 'x' for now. This concept is important though, and we'll come back to it later.

Solve for R_eq (of the three resistor circuit) in terms of R and x.

Now suppose you were going to take an Ohmmeter and measure x. Rip away the two R resistors on the right, and take a look at the new big circuit. Now look at the circuit closely. Recall that both circuits go out to infinity and end up with infinite valued resistors at the far left end (both the new and old big circuits are the same in that respect). The new big circuit (with the equivalent resistance of 'x') is the same as the old big circuit, except with all the resistor values doubled! That means,

x = 2R_eq

Well, you already have a function for R_eq in terms of R and x, so multiply it by 2 and set the result equal to x, and solve for x.

After that you can get an expression for R_eq as a function of R alone (without being a function of x). (Hint: R_eq = x/2 )

 

[physicsforus]

I think I understand. (I have never done this sort of thing before, so please don't get too irritated)


R_eq= R/n

So given that R=25 ohms

I take 25/3=8.33 ohms

x=2(8.33)=16.67 ohms

Am I close at all? or am I still not understanding?

 

[collinsmark]

I think I understand. (I have never done this sort of thing before, so please don't get too irritated)


R_eq= R/n

So given that R=25 ohms

I take 25/3=8.33 ohms

x=2(8.33)=16.67 ohms

Am I close at all? or am I still not understanding?

Sorry, but that's not what I meant.

Starting with original circuit, consider that 2R resistor and everything to the left of it, has a combined equivalent resistance of x. See the figure below.

Next find the equivalent resistance, which we call R_eq, across the nodes AB.
[You have one resistance R in parallel with another resistance (R + x). Find the parallel resistance of R and (R + x). Express this equivalent resistance, R_eq, in terms of R and x.]

Note that in general, two resistances in series take the form,

$$R_s = R_1 + R_2$$

And two resistances in parallel take the form,

$$R_{||} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2}}$$

Does that make more sense?

 

[physicsforus]

Does that make more sense?

Thanks for your help, but I am still completely confused. This was for a game I am playing with a bunch of people and we are allowed to use any resources. I was hoping to learn something new, but this is way over my head. Hopefully one of the other people will understand all of this.

Thanks again.

 

[collinsmark]

Thanks for your help, but I am still completely confused. This was for a game I am playing with a bunch of people and we are allowed to use any resources. I was hoping to learn something new, but this is way over my head. Hopefully one of the other people will understand all of this.

Thanks again.

Don't give up yet.

There's a little bit more math involved, but let me get you started.

$$R_{eq} = \frac{1}{\frac{1}{R} + \frac{1}{R+x}}$$

Do a little algebra, then go back to my previous post.

[Edit: Or perhaps better yet, go back to my previous post first and then do a little algebra.]

 

[physicsforus]

$$R_{eq} = \frac{1}{\frac{1}{25} + \frac{1}{25+x}}$$

R_eq=1/.08x

R_eq=12.5x

x=2(12.5x)

x=25x

x + -25x= 25x + -25x
x+-25x =0
-24x=0
x=0

so between A and B there is no resistance?

(my algebra may be a little rusty especially at 5:20 in the morning)

 

[physicsforus]

I know 0 ohms is not right.

so new calculations:

1
________
1 + 1 + 1
_ __ __ = 3 25x
25 25 X ___ = ____ = 8.3333X

25x 3



Now I have just confused myself...grrrr. so frustrating.

 

[collinsmark]

It might just be easier to keep things in terms of R and x for now (although not really necessary -- you could substitute in the 25 Ohm if you wish).

$$R_{eq} = \frac{1}{\frac{1}{R} + \frac{1}{R+x}}$$

$$= \frac{1}{\frac{R+x}{R(R+x)} + \frac{R}{R(R+x)}}$$

$$= \frac{1}{\frac{R+x+R}{R(R+x)}}$$

$$= \frac{1}{\frac{x+2R}{R(R+x)}}$$

$$= \frac{1}{\frac{x+2R}{R^2 + Rx}}$$

which becomes,

$$R_{eq} = \frac{R^2 + Rx}{x+2R}$$

Now look at your original circuit again (the one you posted in the original post). What we called x is the same thing as if the two rightmost R resistors were removed. It should be obvious to you that the result is that x = 2R_eq. If this isn't obvious immediately, keep looking at the circuit, and think about it for a few minutes. It's because what we are calling x is the same thing as R_eq, except with all the resistor values doubled!

In other words,

$$x = 2 \left( \frac{R^2 + Rx}{x+2R} \right)$$

Solve for x.

As a final step, get back to your R_eq, noting that R_eq = x/2.
(Or alternately, noting that x = 2R_eq, make that substitution beforehand and solve for R_eq directly.)By the way, in case you haven't seen this:
http://xkcd.com/356/

 

[physicsforus]

By golly, Jeeves I think I have it.


I did the Math and got

-25$$\sqrt{}2$$

which broke down to
-35.3553/2

which came to
-17.67767ohms

(or that might be positive not quite sure)


That is actually the second time I got some kind of nerd snipe thing because of this question. Besides those two times, I never seen it before. (No more physics for me. I am sticking to chemistry and biology)

 

[collinsmark]

By golly, Jeeves I think I have it.


I did the Math and got

-25$$\sqrt{}2$$

which broke down to
-35.3553/2

which came to
-17.67767ohms

(or that might be positive not quite sure)

Yes, it's positive. R_eq = 17.6776... Ohms.

And good job! http://www.websmileys.com/sm/cool/653.gif

That is actually the second time I got some kind of nerd snipe thing because of this question. Besides those two times, I never seen it before. (No more physics for me. I am sticking to chemistry and biology)

'Nothing wrong with chemistry and biology. But physics is phun! http://www.websmileys.com/sm/cool/717.gif