Equivalent Resistance of Infinite Resistor Chain

[Saitama]

Homework Statement

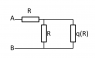
What is the equivalent resistance of the infinite resistor chain, shown in the figure, between the points A and B? Plot the equivalent resistance versus q graph.

[PLAIN]http://www.komal.hu/kep/abra/e4/b2/0d/cec528140d62b825f84ecf4d8.gif[/CENTER]

Homework Equations

The Attempt at a Solution

If q is equal to 1, it is a very easy problem but I have no idea if q is not equal to 1. There is probably a trick to solve this problem but I honestly have no clue about it.

Any help is appreciated. Thanks!​

 

[voko]

Let the resistance of the entire chain be $s(R)$. Now, the chain can be split into two sub-chains: one having resistor R (the one with the A terminal) and the other having everything else. These two chains are connected in series to each other, so $s(R) = R + p(R)$, where $p(R)$ is the resistance of the second sub-chain. The second sub-chain can also be split similarly, this time into sub-chains connected in parallel. So what is $p(R)$? Can it be related to $s(R)$?

 

[Saitama]

Let the resistance of the entire chain be $s(R)$. Now, the chain can be split into two sub-chains: one having resistor R (the one with the A terminal) and the other having everything else. These two chains are connected in series to each other, so $s(R) = R + p(R)$, where $p(R)$ is the resistance of the second sub-chain. The second sub-chain can also be split similarly, this time into sub-chains connected in parallel. So what is $p(R)$? Can it be related to $s(R)$?

I am not sure if I get it. I split p(R) into two parallel resistors R and q(R). Then

$$p(R)=\frac{R\cdot q(R)}{R+q(R)}$$

Hence,

$$s(R)=R+p(R)=R+\frac{R\cdot q(R)}{R+q(R)}$$

Is this what you ask?

 

[voko]

Very well. Now look at the sub-chain whose resistance you denoted with $q(R)$. How is it different from the whole chain, of resistance $s(R)$?

 

[Saitama]

Very well. Now look at the sub-chain whose resistance you denoted with $q(R)$. How is it different from the whole chain, of resistance $s(R)$?

s(R) starts with a resistance of R and q(R) starts with a resistance of Rq. I am still lost, do I write q(R)=s(qR)?

 

[voko]

If you do that, would you be able to relate $s(qR)$ with $s(R)$?

 

[Saitama]

If you do that, would you be able to relate $s(qR)$ with $s(R)$?

Rearranging the equation:

$$s(qR)=\frac{R(s(R)-R)}{2R-s(R)}$$

I am clueless about the next step.

 

[voko]

The next step would be to answer my question in #6.

Say you have a bunch of resistors connected in some weird ways. You know their equivalent resistance is $s$. Now you just multiply their resistances by $q$ uniformly. What is the equivalent resistance of that?

 

[Saitama]

Say you have a bunch of resistors connected in some weird ways. You know their equivalent resistance is $s$. Now you just multiply their resistances by $q$ uniformly. What is the equivalent resistance of that?

$qs$?

 

[voko]

Would you be able to prove or at least justify that?

 

[Saitama]

Would you be able to prove or at least justify that?

I tried what you said with small number of resistors and made different kind of connections, I always got qs but I guess there is a better proof?

I plugged in s(qR)=qs(R) and got the required answer. Thanks a lot voko!

 

[Curious3141]

Pranav, I think what's throwing you off here is that the resistances are varying from node to node. But it's really a simple pattern in disguise.

The "normal" infinite ladder with uniform resistances is solved by taking:

$$Z = R + R||Z$$

where $Z$ is the effective resistance and $||$ denotes the equivalent parallel resistance. The quadratic formula will quickly give you a nice expression related to the golden ratio.

How did you arrive at that insight? By "blocking" the first two resistors with your hand and observing that the remaining infinite net is identical to what you started with, right?

This problem is practically the same. Block the first two resistors (both with resistance R), and you're left with an infinite net. Here, the resistance of the remaining infinite net is not quite the same as what you started with, but it's related quite simply to it (Voko's been guiding you to it). Just set up the quadratic using this info.

 

[voko]

Just our of my curiosity, you said that with $q = 1$ the problem was very simple. I should have asked you before, but anyway, what was your solution?

 

[Saitama]

Pranav, I think what's throwing you off here is that the resistances are varying from node to node. But it's really a simple pattern in disguise.

The "normal" infinite ladder with uniform resistances is solved by taking:

$$Z = R + R||Z$$

where $Z$ is the effective resistance and $||$ denotes the equivalent parallel resistance. The quadratic formula will quickly give you a nice expression related to the golden ratio.

How did you arrive at that insight? By "blocking" the first two resistors with your hand and observing that the remaining infinite net is identical to what you started with, right?

This problem is practically the same. Block the first two resistors (both with resistance R), and you're left with an infinite net. Here, the resistance of the remaining infinite net is not quite the same as what you started with, but it's related quite simply to it (Voko's been guiding you to it). Just set up the quadratic using this info.

Hi Curious3141! :)

Thank you for the insight.

I have solved the problem with the help from voko. I think the key to this problem was to realize s(qR)=qs(R). Rest of the job is very similar to the q=1 case.

Just our of my curiosity, you said that with $q = 1$ the problem was very simple. I should have asked you before, but anyway, what was your solution?

Yes, q=1 case is a simple one probably because I have solved that case more than 10 times.

The solution for q=1 case is outlined by Curious3141. For the current problem, I followed your advice and I finally ended up with a quadratic and solving it gives the right answer (I neglected the negative root). Thank you once again.

EDIT: Oh, the final answer is:

$$\left(1-\frac{1}{2q}+\sqrt{1+\frac{1}{4q^2}}\right)R$$

 

[voko]

The solution for q=1 case is outlined by Curious3141.

This is the basically the same solution then. The only difference is that you end up with the $s(qR)$ term and you need to figure out how it is related to $s(R)$.

As you have seen, simple examples all support that $s(qR) = qs(R)$. A proof (as far as proofs go in physics) could make use of dimensional analysis. Our units for resistance always have some arbitrary factor. By changing that factor, we change the units. But that change must be one and the same for simple resistors and their networks. It is intentionally somewhat vague so that you could think about it yourself :)