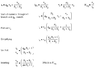NHLspl09
- 96
- 0
Starting the last problem on my EE summer homework assignment for the Fall semester, I wanted to post my thoughts on how to find the resistances before I went ahead and did all the work. I am given what seems to be a fairly simple circuit and asked to find two resistances.
(Attachment 1 - EE P2)
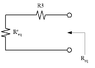
Derive an expression for the resistances, R'eq and Req, for the small-signal circuit shown below.
(Attachment 2 - EE P2.1)
My thought process is exactly what I have written:
Any thoughts or input/am I wrong in doing this?
Homework Statement
(Attachment 1 - EE P2)
Derive an expression for the resistances, R'eq and Req, for the small-signal circuit shown below.
Homework Equations
The Attempt at a Solution
(Attachment 2 - EE P2.1)
My thought process is exactly what I have written:
- Solve for R'eq - First R1 and R2 are in series, and then the result is in parallel with GmVx
- Req = R'eq in parallel with R3
Any thoughts or input/am I wrong in doing this?
 so just to be sure there's no confusion and to answer your questions/statements - the current through the resistors is Vo/(R1+R2)
so just to be sure there's no confusion and to answer your questions/statements - the current through the resistors is Vo/(R1+R2)