Finding Speed, Velocity, Displacement, etc. from velocity-time graphs?

[rayj098]

Lets say I had these two graphs:

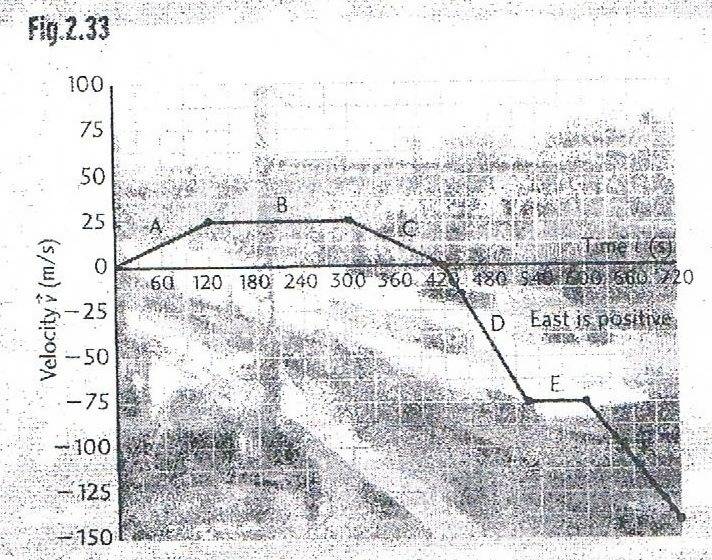
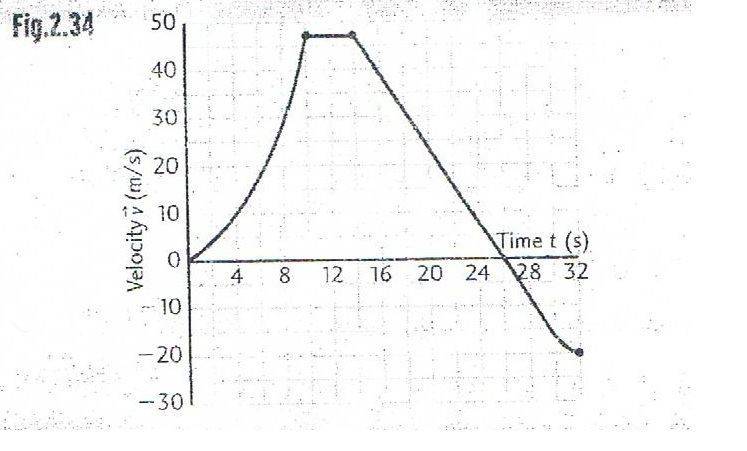
How would I find distance traveled, displacement, speed and velocity from these graphs?


I would appreciate it if you could show your work.


Thanks in advance.

 

[Ignea_unda]

As this is posted in the coursework section, I am assuming this is homework for a class. As such, please follow the template that was provided and include relevant equations and your best attempt. We are more than happy to help you, but need to know where you're getting stuck before we can offer advice.