Finding the determinant of a matrix using determinant properties

[Bolter]

Homework Statement

See below

Relevant Equations

None

Hi, I have been having some trouble in finding the determinant of matrix A in this Q

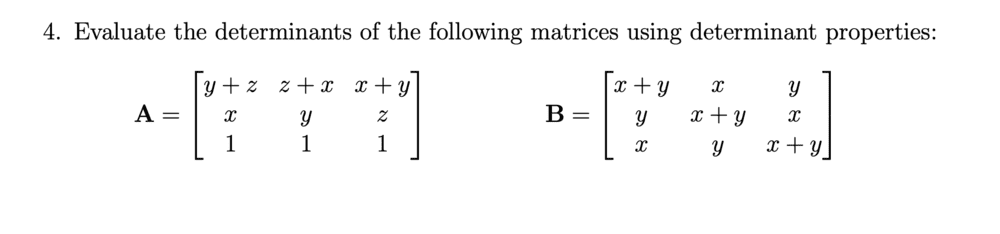
Which relevant determinant property should I make use of to help me find the determinant of matrix A and maybe matrix B also

This is what I have tried for matrix A so far but it's not much help really

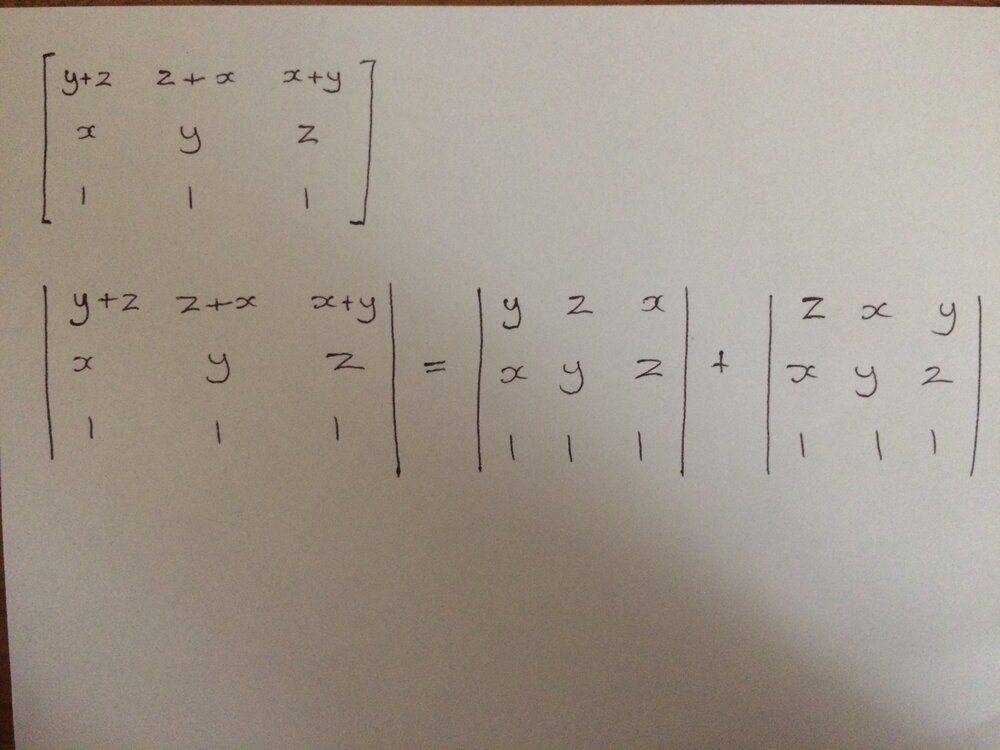
Any help would be much appreciated! Thanks

 

[PeroK]

What you have assumed is definitely not a property of the determinant: $det(X + Y) \ne det(X) + det(Y)$. Absolutely not!

 

[Mark44]

The determinant properties the problem is talking about are row operations or column operations.
If you swap two rows, it changes the sign of the determinant.
If you replace a row by itself + another row, the value remains the same.
If you replace a row by itself times a nonzero constant multiple, the value of the determinant gets multiplied by that value.

The column operations are similar, with "row" above replaced by "column".

 

[Bolter]

What you have assumed is definitely not a property of the determinant: $det(X + Y) \ne det(X) + det(Y)$. Absolutely not!

I thought I was using the addition property which I saw in my notes

 

[PeroK]

I thought I was using the addition property which I saw in my notes

View attachment 270011

Apologies, I missed what you had done there.

 

[Bolter]

The determinant properties the problem is talking about are row operations or column operations.
If you swap two rows, it changes the sign of the determinant.
If you replace a row by itself + another row, the value remains the same.
If you replace a row by a nonzero multiple of itself, the value remains the same.
Edit: If you replace a row by itself times a nonzero constant multiple, the value of the determinant gets multiplied by that value.

The column operations are similar, with "row" above replaced by "column".

For the last bit "If you replace a row by a nonzero multiple of itself, the value remains the same." is that the same as saying if one of the row of a matrix is multiplied by a factor, then the determinant of the matrix will be multiplied by this factor.

as in this rule?

Also I'm not sure which property to start off with which will help me identify what the determinant will be

 

[Bolter]

Apologies, I missed what you had done there.

No worries! Just a bit confused which property I can firstly use that will help break down the matrix to a simpler one so I can find the determinant

 

[Mark44]

For the last bit "If you replace a row by a nonzero multiple of itself, the value remains the same."

I should have said that the value of the determinant is multiplied by the value of that multiple; i.e., if you multiply a row by a constant k, the determinant will be multiplied by the same amount.

I'll edit my earlier reply.

 

[Mark44]

Regarding your work in post #1. What happens if you add row 2 to row 1?

 

[etotheipi]

For your first example I would do $$
\begin{vmatrix}
y+z & z+x & x+y\\
x & y & z\\
1 & 1& 1
\end{vmatrix} =
\begin{vmatrix}
x+y+z & x+y+z & x+y+z\\
x & y & z\\
1 & 1& 1
\end{vmatrix}
$$That's just a matrix with determinant of the form $\begin{vmatrix} a & a & a\\ b_1 & b_2 & b_3 \\ c & c& c \end{vmatrix}$.

 

[epenguin]

NB etothepi did a part for you - he doesn't mean stop there.

As well as the rules in #3 there is also one about linear combination of rows or of columns which is surely in your textbook, with illustrative examples.

 

[Bolter]

For your first example I would do $$
\begin{vmatrix}
y+z & z+x & x+y\\
x & y & z\\
1 & 1& 1
\end{vmatrix} =
\begin{vmatrix}
x+y+z & x+y+z & x+y+z\\
x & y & z\\
1 & 1& 1
\end{vmatrix}
$$That's just a matrix with determinant of the form $\begin{vmatrix} a & a & a\\ b_1 & b_2 & b_3 \\ c & c& c \end{vmatrix}$.

Hi, I can see what you have did here
So the steps are...

Add row 2 to row 1 which you have shown
then I can multiply row 3 by x+y+z
That gives row 1 and 3 to be identical
then minus row 1 from row 3 to get a zero row

Having a zero row would give a zero determinant. Is that ok?

 

[etotheipi]

That's fine. If $\begin{vmatrix} a & a & a\\ b_1 & b_2 & b_3 \\ c & c& c \end{vmatrix} = k$ for non-zero $a$ & $c$, then $\begin{vmatrix} a & a & a\\ b_1 & b_2 & b_3 \\ a & a& a \end{vmatrix} = \frac{ak}{c}$. Switching the first and third rows should negate the sign, however evidently you'd just end up with the same matrix, which means that its determinant must be zero. It follows that $\frac{ak}{c} = 0 \implies k=0$.

 

[Mark44]

Having a zero row would give a zero determinant. Is that ok?

Yes. You can determine this in two ways:
1) Using whatever technique you have for evaluating a determinant.
2) If $\begin{vmatrix}a_1 & a_2 & a_3\\ b_1 & b_2 & b_3 \\0 & 0& 0\end{vmatrix} = D$, then multiplying the third row by nonzero k leaves the values in the third row unchanged, but changes the value of the determinant to kD.

$k\begin{vmatrix}a_1 & a_2 & a_3\\ b_1 & b_2 & b_3 \\0 & 0& 0\end{vmatrix} = \begin{vmatrix}a_1 & a_2 & a_3\\ b_1 & b_2 & b_3 \\0 & 0& 0\end{vmatrix} = kD$
Since the matrix we're taking the determinant is the same, it must be that kD = D, or D(k - 1) = 0. So either k = 1 or D = 0. The choice of k is completely arbitrary, so it must be that D = 0.