rugerts
- 153
- 11
Homework Statement
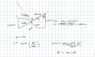
Given weight car = 2500lb, acceleration = constant = 2 ft/s^2, radius of curvature at C = 1000 ft, distance between A and B = 1300 ft, distance between B and C = 900 ft
Find horizontal force of road on car at B and C.
Homework Equations
F = ma in normal-tangential coordinate system
The Attempt at a Solution
I tried using kinematics, since I've got constant acceleration, to find the velocity, in order to use that to find the centripetal force. From there, I'm trying to find the Normal force. I'm using normal tangential coordinate system. I'm having trouble recognizing the geometry of the situation, since I seem to need to know angles. I tried using the arc sector formula. The answer I'm getting is way off of the one shown below in the image.
(Ignore the cos(0.9), that's in radians by accident. I forgot to change that on the image)