VaioZ
- 19
- 0
Hello first time posting in the Physics forum!
1. Homework Statement
A varsity player is attempting to make a shot. The ball leaves the hands of the player at an angle of 50 degrees to the horizontal at an elevation of 2 meters above the floor. The skillful player makes the shot with the ball traveling precisely through the center of the ring (8 meters from the player and 3 meters above the floor). To loud cheers, calculate the speed at which the ball left the hands of the player. Sketch the problem!
Y=Vot-1/2g(t)^2
Voy = Vosintheta
Vox = Vocostheta
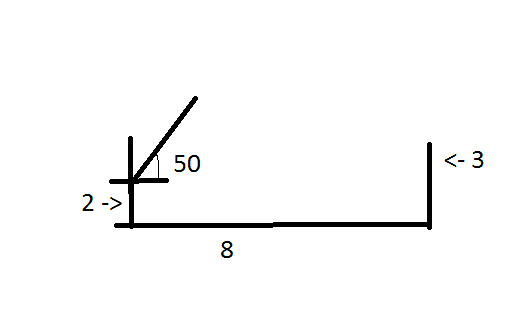
Vox = Vocostheta -> 8=Vocos(50degrees) -> Vo=12.446m/s
Then I plug it to X=Vot+1/2at^2 a is always 0 right? So it becomes X=Vot -> X=12.446(t) -> t=(0.643s)
Then I plug the time to the y equation of free fall.. Delta Y is 1 right? Because 3-2=1
Y=Vot-1/2gt -> 1=Vo(0.643)-1/2(9.8)(0.643)^2 Vo=4.7059m/s
y
I'm not sure if my answer is right.. if not can someone guide me...
If it is wrong sorry If I got a wrong answer.. This is why I post in this forums.
1. Homework Statement
A varsity player is attempting to make a shot. The ball leaves the hands of the player at an angle of 50 degrees to the horizontal at an elevation of 2 meters above the floor. The skillful player makes the shot with the ball traveling precisely through the center of the ring (8 meters from the player and 3 meters above the floor). To loud cheers, calculate the speed at which the ball left the hands of the player. Sketch the problem!
Homework Equations
Y=Vot-1/2g(t)^2
Voy = Vosintheta
Vox = Vocostheta
The Attempt at a Solution
Vox = Vocostheta -> 8=Vocos(50degrees) -> Vo=12.446m/s
Then I plug it to X=Vot+1/2at^2 a is always 0 right? So it becomes X=Vot -> X=12.446(t) -> t=(0.643s)
Then I plug the time to the y equation of free fall.. Delta Y is 1 right? Because 3-2=1
Y=Vot-1/2gt -> 1=Vo(0.643)-1/2(9.8)(0.643)^2 Vo=4.7059m/s
y
I'm not sure if my answer is right.. if not can someone guide me...
If it is wrong sorry If I got a wrong answer.. This is why I post in this forums.