Finding the magnitude of Torque

  • Thread starter Thread starter nina123
  • Start date Start date
  • Tags Tags
    Magnitude Torque
AI Thread Summary
To calculate the torque produced by a force of 75.0 N applied at an angle of 35.0° to a box with dimensions 2.51 m by 1.62 m, the correct approach involves using the torque formula t = rFsinθ, where θ is the angle between the radial vector and the force direction. The radial vector connects point O to the point of force application. It is crucial to determine this angle accurately, as it differs from the angle of the force with respect to the horizontal. This adjustment is necessary because the torque calculation changes when the angle is not 0° or 90°. Understanding the geometry of the situation is key to solving the problem correctly.
nina123
Messages
5
Reaction score
0

Homework Statement



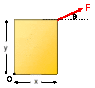
A force F = 75.0 N is applied to a box with dimensions y = 2.51 m, x = 1.62 m. The force is applied at an angle θ with respect to the horizontal. For θ = 35.0°, calculate the magnitude of the torque produced by F about the point O.
(reference attached picture)

Homework Equations



t=rFsinθ=r\botF=rF\bot

The Attempt at a Solution



For the other questions like this i just used t=rF when the angles were 0 and 90deg.
but now that it is at a 35deg angle the same formula doesn't work.

HELP PLEASE?
 

Attachments

  • torque1.gif
    torque1.gif
    2.7 KB · Views: 902
Physics news on Phys.org
In your formula for the torque, the angle θ corresponds to the angle between the radial vector (connecting the points O and F) and the direction of the force.
In your image, draw this radial vector and then you can see what the angle between the radial vector and the force is. Use this angle in the formula.
 
Thanks!
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Calculation of resulting force from out of axis Torque
Replies
21
Views
3K
Solid disk frictional torque magnitude
Replies
9
Views
3K
How to calculate the magnitudes of three forces around a hexagon
Replies
17
Views
2K
Where on a rigid body is a resultant force applied?
Replies
11
Views
1K
Calculate Torque About Axis B: F, θ, ϕ, π Involved
Replies
3
Views
4K
Finding the Torque on a Fixed Square
Replies
7
Views
2K
Frequency & Wavelength of a Vibrating Wire
Replies
5
Views
1K
Find the torque for a vehicle wheel
Replies
2
Views
1K
Question about Normal Force and Torque
Replies
5
Views
3K
I Question regarding finding the magnitude of Torque
Replies
4
Views
1K

Hot Threads

Recent Insights

Back
Top