javii
- 23
- 0
Homework Statement
Homework Equations
r=sqrt(a^2+b^2)
θ=arg(z)
tan(θ)=b/a
The Attempt at a Solution
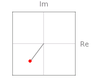
for a)[/B]
finding the polar form:
r=sqrt(-3^2+(-4)^2)=sqrt(7)
θ=arg(z)
tan(θ)=-4/-3 = 53.13 °
300-53.13=306.87°
-3-j4=sqrt(7)*(cos(306.87+j306.87)
I don't know if my answer is correct because it is given that -π<arg(z)<=π