pturo
- 3
- 0
The problem statement
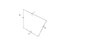
A uniform rod of length 2m and mass 5kg is connected to a vertical wall by a smooth hinge at A and a wire CB as shown. If a 10 Kg mass is attached to D, find:
a) the tension in the wire
b) the magnitude of the reaction at the hinge A.
attached is my copy of the diagram from the textbook, (with forces added by me) and a force diagram
The tension in the wire will be the anticlockwise moment about A. This is balanced by the clockwise moment - which comes from the weight of the beam and the mass attached to the end.
Clockwise moments 49 cos 26.77^\circ + 98 * 2 cos 26.77^\circ =218.74N
Anticlockwise moment: 0.5 T
0.5T = 218.74N
T = 437.5N
It is the next part where I am unsure. I need to get the magnitude of the reaction force at A. This is going to be a result of what I've called force D, which runs along AD.
I have illustrated the forces diagram in the attachment and the thing that is confusing me is that the weight force is apparently the largest on in the triangle. But from the forces in the original diagram, tension is a larger force that the combined weights.
As far as I can see there are no other forces acting on the system.
Can anyone give me some pointers as to where my thinking on this is going wrong/what my approach should be for finding the force along AD, and thus the reaction at A?
I would be very grateful for any information!
A uniform rod of length 2m and mass 5kg is connected to a vertical wall by a smooth hinge at A and a wire CB as shown. If a 10 Kg mass is attached to D, find:
a) the tension in the wire
b) the magnitude of the reaction at the hinge A.
attached is my copy of the diagram from the textbook, (with forces added by me) and a force diagram
The Attempt at a Solution
The tension in the wire will be the anticlockwise moment about A. This is balanced by the clockwise moment - which comes from the weight of the beam and the mass attached to the end.
Clockwise moments 49 cos 26.77^\circ + 98 * 2 cos 26.77^\circ =218.74N
Anticlockwise moment: 0.5 T
0.5T = 218.74N
T = 437.5N
It is the next part where I am unsure. I need to get the magnitude of the reaction force at A. This is going to be a result of what I've called force D, which runs along AD.
I have illustrated the forces diagram in the attachment and the thing that is confusing me is that the weight force is apparently the largest on in the triangle. But from the forces in the original diagram, tension is a larger force that the combined weights.
As far as I can see there are no other forces acting on the system.
Can anyone give me some pointers as to where my thinking on this is going wrong/what my approach should be for finding the force along AD, and thus the reaction at A?
I would be very grateful for any information!