bsr25
- 7
- 0
Homework Statement
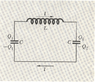
The figure opposite shows a free oscillator composed of an LC circuit. Derive an expression for the resonance frequency. Show all of your working.
Homework Equations
d2x/dt2 + ω2x = 0
The Attempt at a Solution
First I tried using Kirchoffs Voltage Law to set up a differential equation defining the circuit.
L(d2q/dt2) + Q1/C + Q2/C = 0
I then combined the two voltages across the capcitor, and divided by L
(d2q/dt2) + QTotal/LC = 0
Comparing this to the equation for SHM:
d2x/dt2 + ω2x = 0
shows that ω2= 1/LC.
But I figure this cannot be the case as that is the result expected for a simple LC circuit with one inductor and one capcitor. As this is two capcitors and one inductor I figure the rsult must be different.
One thing I notice on the diagram is the Capcitors have both negative plates facing each other, I wasnt sure what effect if any this would have on the circuit.
Other than this attempt at a solution which I am fairly sure if way off, I am a bit lost. Any help towards reahcing the right answer would be greatly appreciated!
Thanks