Finding the resultant force on the block

[ameliapond]

Homework Statement

Hi all, I've been given a question for homework and I am not 100% sure how to do it exactly!
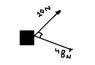
I have included a diagram or the situation

Homework Equations

The question is Find the resultant force on the block (picture attached)

The Attempt at a Solution

What i did was, split it into 2 right angled triangles and used trig to determine the resultant force. do i add the two together to get the resultant force?

 

[CWatters]

If adding vectors at right angles you can use pythagorous

c² = a² +b²

to work out the magnitude.

Try drawing the 20N vector as if it was attached to the other end of the 48N vector.

 

[ameliapond]

so the resultant is the line that would connect the two vectors?

 

[NascentOxygen]

so the resultant is the line that would connect the two vectors?

As you have drawn them, the tail of one is connected to the tail of the other.

To perform a vector addition:
you translate one of the vectors, (i.e., using a sliding transformation) so that the tip of one arrow connects to the tail of the other. Then you draw a third arrow from the tail of that combo to its tip, and this third arrow represents the vector sum of that pair. Use your knowledge of trig to find its length. (As a check: if you draw them accurately to scale and preserve angles, your calculated value should agree with your measured value.)

 

[CWatters]

scroll down this page..

http://www.physicsclassroom.com/class/vectors/u3l1b.cfm

EDIT: Actually the parallelagram rule is probably more general. Pythagorous only works where the vectors are at right angles..

http://www.engineeringtoolbox.com/vector-addition-d_320.html