Finding the Right Answer: Tips for Solving Oscillation Problems

[xtrubambinoxpr]

I apologize ahead of time for all of these post about oscillation. I am trying to learn this stuff on my own.

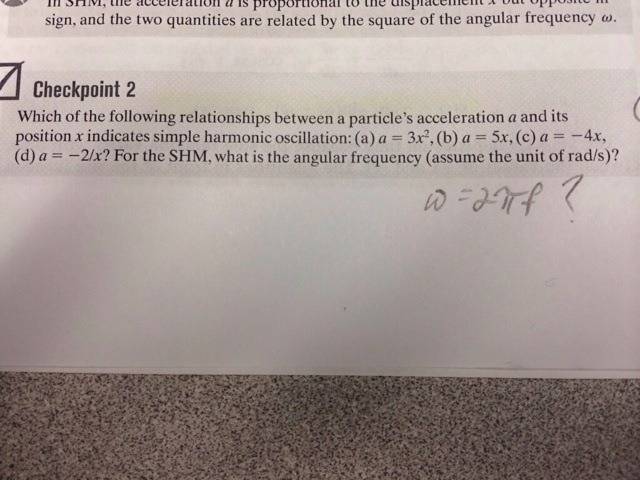
I answered "a" because the x^2 function. But I don't know the second part.. Would it also be 3x^2 because it is proportional to the x(t) function?

 

[nasu]

What type of force acts in a SHO? What is the dependence on displacement?

 

[xtrubambinoxpr]

What type of force acts in a SHO? What is the dependence on displacement?

depends on the force being acted on it?

 

[nasu]

What depends on the force? I don't understand this.

Imagine a simple harmonic oscillator. You displace it from equilibrium by a distance x.
What force acts to bring it back to equilibrium? What is the dependence of this force of x?
You can think about a specific system, like a ball attached to a spring. In this case the force is the elastic force isn't it?

 

[xtrubambinoxpr]

The gravity would be pulling it down and the force would be opposite.
Or with a block the spring is applying the force if it's on a table both ways. Acceleration will be applied opposite of the motion. So the force is given by the spring

 

[Chestermiller]

Or with a block the spring is applying the force if it's on a table both ways. Acceleration will be applied opposite of the motion. So the force is given by the spring

Good. If the spring stretches by x, what is the force that the spring exerts on the mass? From Newton's second law, what is the acceleration (as a function of the spring constant, the mass of the mass, and the displacement from equilibrium x)?

 

[xtrubambinoxpr]

Good. If the spring stretches by x, what is the force that the spring exerts on the mass? From Newton's second law, what is the acceleration (as a function of the spring constant, the mass of the mass, and the displacement from equilibrium x)?

You lost me. Only using the spring formulas or the oscillation ones? I don't see the connection. If F=kx. Then kx/m=a

 

[Chestermiller]

You lost me. Only using the spring formulas or the oscillation ones? I don't see the connection. If F=kx. Then kx/m=a

Actually, it looks like you do see that connection. You just didn't realize it. These are the equations I was asking about. Actually, the equation for the acceleration should have a minus sign, because the spring is a restoring force constantly trying to bring the mass back to the equilibrium position; but the mass always overshoots the equilibrium position. Back to the equation for the acceleration: a = -kx/m. Look at your problem statement now, and see which relationship between the acceleration and the displacement agrees with this equation.

Now, back to the relationship between this and SHM. The acceleration is the second derivative of the displacement with respect to time, so we have:
$$a=\frac{d^2x}{dt^2}=-\frac{k}{m}x$$
The complimentary solution to this differential equation is:

x=A sin(ωt) + Bcos(ωt)

where $ω=\sqrt{\frac{k}{m}}$

The constants A and B in the equation depend on the initial displacement and the initial velocity of the mass.

Do you see now how this ties in with SHM?

Chet

 

[xtrubambinoxpr]

Actually, it looks like you do see that connection. You just didn't realize it. These are the equations I was asking about. Actually, the equation for the acceleration should have a minus sign, because the spring is a restoring force constantly trying to bring the mass back to the equilibrium position; but the mass always overshoots the equilibrium position. Back to the equation for the acceleration: a = -kx/m. Look at your problem statement now, and see which relationship between the acceleration and the displacement agrees with this equation.

Now, back to the relationship between this and SHM. The acceleration is the second derivative of the displacement with respect to time, so we have:
$$a=\frac{d^2x}{dt^2}=-\frac{k}{m}x$$
The complimentary solution to this differential equation is:

x=A sin(ωt) + Bcos(ωt)

where $ω=\sqrt{\frac{k}{m}}$

The constants A and B in the equation depend on the initial displacement and the initial velocity of the mass.

Do you see now how this ties in with SHM?

Chet

So, if I understand this completely, I was wrong because there is no x^2 in regards to the acceleration. it would be the -4x option because it seems to be closely related to what we just proved. I think I was thinking of ω$^{2}$

 

[sophiecentaur]

You lost me. Only using the spring formulas or the oscillation ones? I don't see the connection. If F=kx. Then kx/m=a

There's a very important minus sign missing in your Force formula.

Have you been set this question without any prior information about SHM and do you have no text to work from?

 

[xtrubambinoxpr]

There's a very important minus sign missing in your Force formula.

Have you been set this question without any prior information about SHM and do you have no text to work from?

I have the text and I now remember the (-) sign in the equation. Completely my mistake. I have 2 books I am trying to learn from so forgive me if I forget something.

 

[sophiecentaur]

Your book (or Wiki) will have it all in there - you may just need to read it more slowly.

What is the relationship (always) between force and acceleration and how can you relate that to your Force equation (with the right sign included). Now look at those alternatives in the question and find one that has the same form as this.

PS Using angular frequency ω, is always annoying and perplexing to start with but it is very useful to get used to it because, once you start to get advanced, if you continue to use frequency f, the constant 2∏ keeps cropping up, multiple times and just gets in the way.

 

[xtrubambinoxpr]

Your book (or Wiki) will have it all in there - you may just need to read it more slowly.

What is the relationship (always) between force and acceleration and how can you relate that to your Force equation (with the right sign included). Now look at those alternatives in the question and find one that has the same form as this.

PS Using angular frequency ω, is always annoying and perplexing to start with but it is very useful to get used to it because, once you start to get advanced, if you continue to use frequency f, the constant 2∏ keeps cropping up, multiple times and just gets in the way.

based on what you're saying now I think it is either 5x or -4x. the force is directly proportional to the acceleration. I think I am missing the final key point

 

[xtrubambinoxpr]

By the way if anyone were to want to skype or google hangout on this topic I would be cool with that too. Just trying to learn.

 

[sophiecentaur]

Why was I so picky about the sign? It tells you the direction that the force is acting in and is essential in the mathematical description of the motion. Which direction is the force? To reduce or increase the magnitude of displacement?

 

[xtrubambinoxpr]

Why was I so picky about the sign? It tells you the direction that the force is acting in and is essential in the mathematical description of the motion. Which direction is the force? To reduce or increase the magnitude of displacement?

it is negative because it is the restoring force to get it back to its initial position

 

[sophiecentaur]

So which of the alternatives is showing that?

 

[xtrubambinoxpr]

So which of the alternatives is showing that?

-4x is the only one abiding by that principle

 

[sophiecentaur]

So, how does that look? A reasonable answer?

 

[xtrubambinoxpr]

So, how does that look? A reasonable answer?

being that it needs to have the equation form to fit, yes I say it is reasonable. a(t) = -ω$^{2}$x(t).. that being said -4x is the only option that seems to fit.

 

[sophiecentaur]

being that it needs to have the equation form to fit, yes I say it is reasonable. a(t) = -ω$^{2}$x(t).. that being said -4x is the only option that seems to fit.

That is a fresh addition. Can you explain where it came from? (I am trying to do this one step at a time.)

 

[xtrubambinoxpr]

That is a fresh addition. Can you explain where it came from? (I am trying to do this one step at a time.)

the position function for a particle in SHM is x(t) = Xmcos(ωt+ø)

differentiating it you get velocity. and again you get a(t) = -ω$^{2}$XmCos(ωt+ø) ... = a(t) = -ω$^{2}$x(t)

 

[sophiecentaur]

Right. So that tells you that ω² equal to what? And hence ω= what?

 

[Chestermiller]

-4x is the only one abiding by that principle

Correct. Nice job of figuring it out.

Chet

 

[xtrubambinoxpr]

Right. So that tells you that ω² equal to what? And hence ω= what?

would it be Sqrt(a(t)/x(t))

 

[Chestermiller]

would it be Sqrt(a(t)/x(t))

If, in general, a= -ω²x, and in your problem a = -4x, what is ω for your problem?

 

[xtrubambinoxpr]

If, in general, a= -ω²x, and in your problem a = -4x, what is ω for your problem?

ω=2 because 2 squared = 4. so just to make sure I am doing -(w*w)(x)
I picked positive 5x before because I was an idiot and thought the negative was attached to the ω value.

 

[Chestermiller]

ω=2 because 2 squared = 4. so just to make sure I am doing -(w*w)(x)
I picked positive 5x before because I was an idiot and thought the negative was attached to the ω value.

Don't be so hard on yourself. You just need to get a little more experience. Like I said earlier, you doped things out pretty well.

Chet

 

[sophiecentaur]

would it be Sqrt(a(t)/x(t))

That is not incorrect - but not what a sneaky teacher would do and doesn't actually give you the answer. It can be so annoying when you're shown the answer and you think "why did he choose to do it that way?". You just develop a feel for how to drag the right answer out of what you have. This time the way through is to substitute information in one equation with info from another - just spotting the similarity of two equations. Another tool for your maths toolbox.

 

[xtrubambinoxpr]

That is not incorrect - but not what a sneaky teacher would do and doesn't actually give you the answer. It can be so annoying when you're shown the answer and you think "why did he choose to do it that way?". You just develop a feel for how to drag the right answer out of what you have. This time the way through is to substitute information in one equation with info from another - just spotting the similarity of two equations. Another tool for your maths toolbox.

Thanks for the input! Appreciate it