Specter
- 120
- 8
Homework Statement
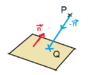
Find the shortest distance from P(-4,2,6) to the plane 2x-3y+z-8=0.
Homework Equations
##|proj_\vec n \vec PQ|=|(\frac {\vec PQ \cdot \vec n} {\vec n \cdot \vec n})| |\vec n|##
The Attempt at a Solution
I kind of had to guess some steps because it was done differently in my lesson and I couldn't figure it out that way. Am I on the right track?
The normal is ##\vec n =(2,-3,1)##
Find another point on the plane, let x=0 and y=0
2x-3y+z-8=0
2(0)-3(0)+z-8=0
z=0
Another point on the plane is Q(0,0,8).
I have to find the direction of ##\vec {PQ}##
##\vec {PQ}=\vec Q - \vec P##
=(0,0,8)-(-4,2,6)
=(4,-2,2)
To find the shortest distance, I think I would project ##\vec {PQ}## onto ##\vec n##.
##|proj_\vec n \vec PQ|=|(\frac {\vec PQ \cdot \vec n} {\vec n \cdot \vec n})| |\vec n|##
=##|\frac {(4,-2,2) \cdot (2,-3,1)} {(2,-3,1) \cdot (2,-3,1)}| |(2,-3,2)|##
=##|\frac {(4)(2)+(-2)(-3)+(2)(1)} {(2)(2)+(-3)(-3)+(1)(1)}| |(2,-3,1)|##
=##|\frac {16} {14}| |(2,-3,1)|##
=##|\sqrt (\frac {16} {7}), (-\frac {24} {7}), (\frac {8} {7})|##
=##\sqrt (\frac {16} {7})^2 + (-\frac {24} {7})^2 + (\frac {8} {7})^2##
=##\sqrt \frac {256} {49} + \frac {576} {49} + \frac {64} {49}##
=##\sqrt \frac {896}{49}##
The shortest distance is ##\sqrt \frac {896}{49}##