uasaki
- 16
- 0
Homework Statement
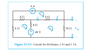
The circuit diagram is attached below.
We're supposed to a) find the Thevenin equivalent circuit and b) find the value of Rl (the load resistor) so that the current flowing through it is 0.5A.
Homework Equations
The Attempt at a Solution
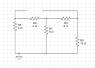
Since the circuit doesn't contain any dependent sources, we can zero out all the independent sources and calculate the Thevenin resistance directly. The 4A current source becomes an open circuit and the 48V voltage source becomes a short. I've attached a picture of what the resulting circuit should look like (it's the circuit2.png file). We can find the equivalent resistance by combining the resistances in series and parallel. Starting from the right, the 6-ohm and 10-ohm resistor are in series, so you can combine them to get a 16-ohm resistor. Then, that 16-ohm resistor is in parallel with the 8-ohm resistor, which is equivalent to a 5.3-ohm resistor. Finally, you can add that 5.3-ohm resistor with the two 4-ohm resistors in order to get an equivalent resistance of 13.3-ohms. Is this calculation correct?
Also, I tried to calculate the short-circuit current flowing from a to b, but I keep getting 0. Is it possible to get 0 for the Thevenin/Norton short-circuit current, or am I missing something?