hms.tech
- 246
- 0
b]1. Homework Statement [/b]
Find the total resistance of this complex combination of resistors.
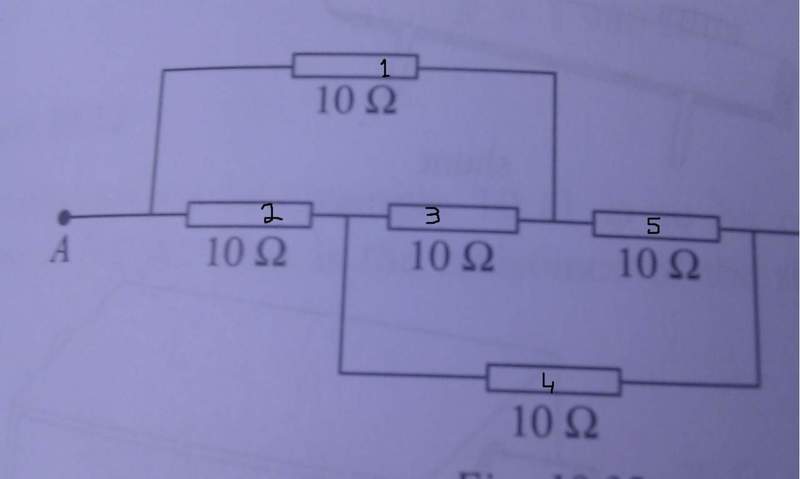 [
[
R(total)= (Rr)/(R+r)
resistance of r(2) and r(3) = 20Ω
resistance of the combination of r(1) and the resultant 20 Ω(ie r(2) and r(3) ) = 20/3
resistance of r(3) and r(5) = 20Ω
resistance of te combination of r(4) and the resultant 20 (ie r(3) and r(5) ) = 20/3
I can't deduce and answer from the above (correct) results.
Need urgent Help !
Find the total resistance of this complex combination of resistors.
Homework Equations
R(total)= (Rr)/(R+r)
The Attempt at a Solution
resistance of r(2) and r(3) = 20Ω
resistance of the combination of r(1) and the resultant 20 Ω(ie r(2) and r(3) ) = 20/3
resistance of r(3) and r(5) = 20Ω
resistance of te combination of r(4) and the resultant 20 (ie r(3) and r(5) ) = 20/3
I can't deduce and answer from the above (correct) results.
Need urgent Help !
