phb1762
- 6
- 0
- Homework Statement
- (a) Construct the matrix for a beam splitter with a 70% reflectivity.
(b) By applying this operation twice, calculate the output state of a single photon in the input. Hint: the second beam splitter can be oriented in two different ways.
- Relevant Equations
- 1) Born rule for bipartite states ( as there are 2 possibilities for input and two probabilities due to the 70:30 beam splitter)
2) ket space equations
Hello,
I have some trouble understanding how to construct the matrix for the beam splitter (in a Mach-Zehnder interferometer).
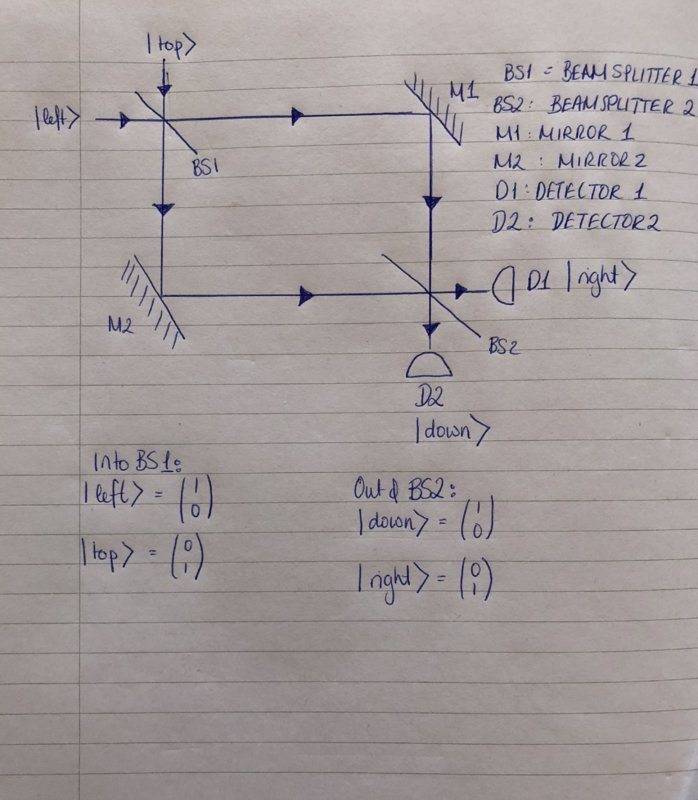
I started with deciding my input and output states for the photon.
I then use Borns rule, which I have attached below:

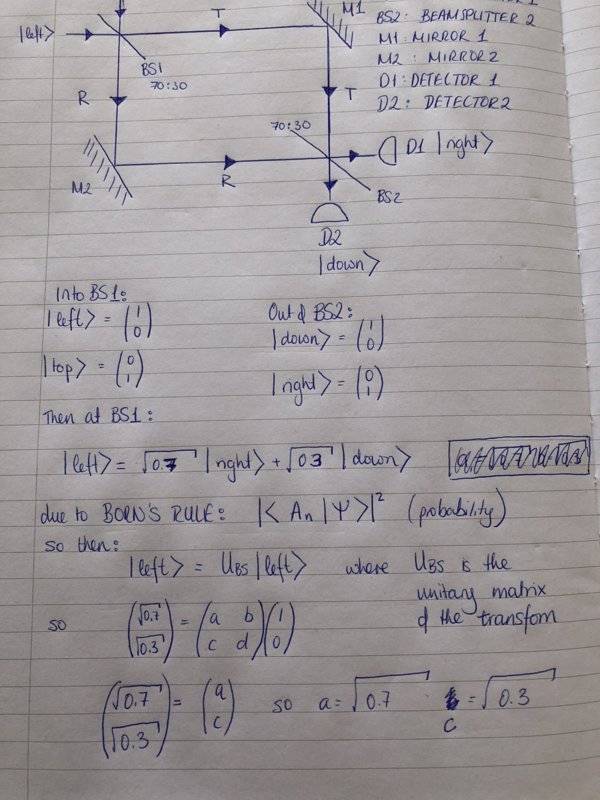
To get the following for the state space of the photon going in:
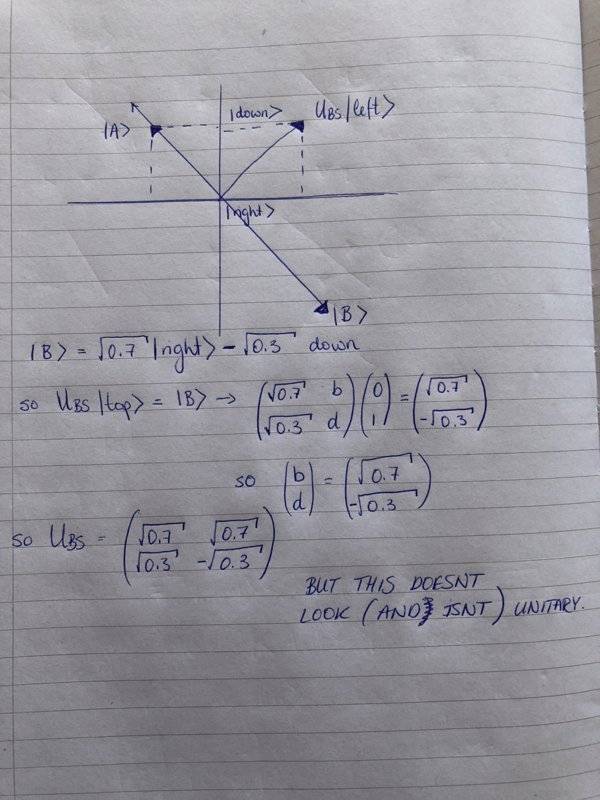
But in the end, I end up with a matrix that doesn't appear unitary:
I don’t know where I’m going wrong. We’ve only just started doing Quantum and the lectures are quite difficult for me to understand. I would appreciate any help and advice as I really would like to be able to do these types of questions as I suspect they will be in my exam!
Thanks everyone in advance and sorry for the many photos!
I have some trouble understanding how to construct the matrix for the beam splitter (in a Mach-Zehnder interferometer).
I started with deciding my input and output states for the photon.
I then use Borns rule, which I have attached below:
To get the following for the state space of the photon going in:
But in the end, I end up with a matrix that doesn't appear unitary:
I don’t know where I’m going wrong. We’ve only just started doing Quantum and the lectures are quite difficult for me to understand. I would appreciate any help and advice as I really would like to be able to do these types of questions as I suspect they will be in my exam!
Thanks everyone in advance and sorry for the many photos!
