LukeStarChief
- 2
- 0
Homework Statement
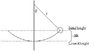
A 2.0 m pendulum is released from rest when the support string is at an angle of 25 degrees with the vertical. What is the speed of the bob at the bottom of the string?
Homework Equations
KE=1/2mv^2
PE=mgh
The Attempt at a Solution
I thought that height would just be 2cos25. Since at the bottom of the pendulum, all PE is converted to KE, PE would equal KE. That makes sense. So my equation was gh=1/2v^2 (Mass cancels). My velocity came out to be .59 m/s and I'm unsure if this is correct or not. Some other sites for this problem talked about height being 2-2cos25. If that is true, why would that be height as opposed to just 2cos25?