tasveerk
- 24
- 0
Homework Statement
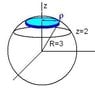
What is the volume of the region above the plane z = 2 and inside the sphere x2 +y2 +z2 = 9.
Homework Equations
The Attempt at a Solution
I am trying to use a spherical triple integral. I am mainly having trouble finding ∅.
This is what I have been trying ∫arccos(2/3)0∫2∏∫32 ρ2sin∅dpdθp∅
The answer is 8∏/3. I am pretty sure there are errors in my setup