- #1
JFuld
- 23
- 0
Homework Statement
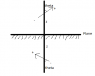
a perfect dipole (p) is situated a distance z above an infinite grounded plane. The dipole is at an angle theta with the perpendicular to the plane. find the torque on p.
if you have griffiths text, its problem 4.6
Homework Equations
E(dipole)= (p/4pi*epsilon.*r^3)*(2cos(theta) r^ +sin(theta) theta^), ^refers to unit vector
torque = PxE
The Attempt at a Solution
Well i can't seem to figure out how to find E.The above equation for E doesn't take into consideration the grounded plate, so i thought maybe i need to solve for the potential first. But the potential on the plate would be zero since it is grounded, so I don't really know what to do with that.
Im not really sure how to approach this honestly, a nudge in the right direction would be appreciated.