odolwa99
- 85
- 0
For part (i), my answer is correct but my answer for (ii) seems to be a little bit out. I can't spot where I've gone wrong. Can anyone help me out?
Many thanks.
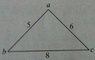
Q. In the given triangle, find (i) |\angle abc|, (ii) |\angle bac|.
(i) cos B = \frac{c^2+a^2-b^2}{2ac} => cos B = \frac{5^2+8^2-6^2}{(2)(8)(5)} => cos B = \frac{53}{80} => B = secant 0.6625 => B = 48^o 31'
(ii) \frac{sin48^o 31'}{6} = \frac{sin x}{8} => \frac{0.7491}{6} = \frac{sin x}{8} => sin x = (8)(0.1249) => x = cosec 0.9989 => x = 87^o42'
Ans.: (From textbook): (i) 48^o 31', (ii) 92^o 52'
Many thanks.
Homework Statement
Q. In the given triangle, find (i) |\angle abc|, (ii) |\angle bac|.
The Attempt at a Solution
(i) cos B = \frac{c^2+a^2-b^2}{2ac} => cos B = \frac{5^2+8^2-6^2}{(2)(8)(5)} => cos B = \frac{53}{80} => B = secant 0.6625 => B = 48^o 31'
(ii) \frac{sin48^o 31'}{6} = \frac{sin x}{8} => \frac{0.7491}{6} = \frac{sin x}{8} => sin x = (8)(0.1249) => x = cosec 0.9989 => x = 87^o42'
Ans.: (From textbook): (i) 48^o 31', (ii) 92^o 52'