Finding V and I in a simple circuit

[Xiao Xiao]

Homework Statement

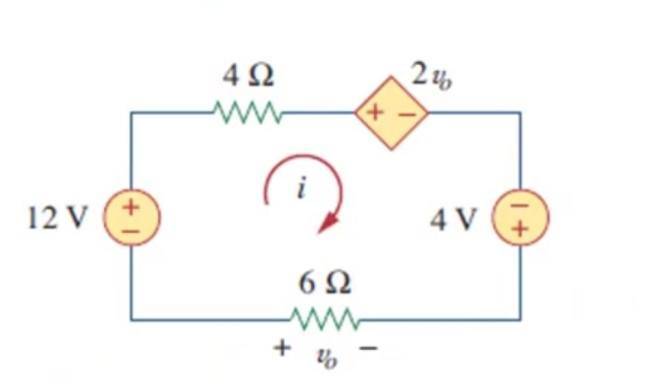
Determine Vo and i in the circuit shown:

Relevant Equations

Kirchhoff's Voltage Law.

So I know I have to use kirchhoff's Voltage Law so when I apply it's:
-12+4i+2Vo-4-Vo=0
and Vo=6i so --> -16+4i+2(6i)-(6i)=0 but apparently that's wrong and Vo should be =-6i and so when I substitute it in the equation it should be
-16+4i+2(-6i)-(-6i)=0 and I don't understand why.

 

[phinds]

You don't have consistency in the + and - signs

 

[Xiao Xiao]

You don't have consistency in the + and - signs

I thought that when applying the law, and I start in the direction of clockwise loop in my example, the current enters the nagetive terminal for the 12V and I started with -, so now any source with current entering the negative terminal, the current will be given a negative sign, and sources with current entering from the positive terminal will be given a positive sign. Am I correct so far? And from what I understood from what understood from my lecture that the application of passive sign convention in Ohm's law in the equation (am I wrong?). I don't get why we put Vo=-6i and not V=6i, are we applying passive sign convention again? I'm sorry it sounds like a stupid question but my lectures aren't clear on it, like the professor wrote Vo=6i but continued with the answer on the slides which was different. And I don't know why type om Google search bar to find an answer.

 

[phinds]

What I would suggest is that you take each element individually and draw an arrow in the direction for which the voltage of that element is positive. Thus the arrow on the 4 ohms, for example, would be left to right with the arrowhead designating positive. When you have done this for each element then just choose a direction around the loop and add or subtract every element based on the arrow.

Having done that, if you still get the wrong answer, then post your diagram with the arrows and we can see where you went wrong.

 

[Xiao Xiao]

What I would suggest is that you take each element individually and draw an arrow in the direction for which the voltage of that element is positive. Thus the arrow on the 4 ohms, for example, would be left to right with the arrowhead designating positive. When you have done this for each element then just choose a direction around the loop and add or subtract every element based on the arrow.

Having done that, if you still get the wrong answer, then post your diagram with the arrows and we can see where you went wrong.

Okay, so I took a long time thinking about it. So, in the original Kirchhoff's equation, we assigned a negative because of the passive sign convention and direction of the loop, but in Ohm's law when we did V=iR we gave it a negative sign because the original current (not just the direction of the loop) is going through the negative terminal so the sign is for the current? So if the current went through the positive terminal I'm Ohm's law it would have been positive but we'd still put a negative in kirchhoff's law because of the direction of the loop?

 

[phinds]

Okay, so I took a long time thinking about it. So, in the original Kirchhoff's equation, we assigned a negative because of the passive sign convention and direction of the loop, but in Ohm's law when we did V=iR we gave it a negative sign because the original current (not just the direction of the loop) is going through the negative terminal so the sign is for the current? So if the current went through the positive terminal I'm Ohm's law it would have been positive but we'd still put a negative in kirchhoff's law because of the direction of the loop?

FORGET (*) direction of individual elements based on Kirchoff. Just take each element individually based on the stated value, or Ohms Law if appropriate, and draw the appropriate arrow. Then it doesn't MATTER which direction you take for the loop, you still get the right answer.

* An over-statement since once you decide on a direction for the loop then you DO have to use the same direction for each element (and that basically IS the Kirchoff loop)

 

[Xiao Xiao]

FORGET (*) direction of individual elements based on Kirchoff. Just take each element individually based on the stated value, or Ohms Law if appropriate, and draw the appropriate arrow. Then it doesn't MATTER which direction you take for the loop, you still get the right answer.

* An over-statement since once you decide on a direction for the loop then you DO have to use the same direction for each element (and that basically IS the Kirchoff loop)

Yes, I get it now, thank you.

 

[boo]

The + and - on Vo mean that you are to subtract the voltage on the negative end from the voltage from the positive end. It is that potential difference that the voltage dependent voltage source is tied to. Since with the given current direction there is a actually a voltage DROP from the minus end to the plus end (passive sign convention) that voltage difference is negative. Thus that voltage is - 6*i.

 

[Xiao Xiao]

The + and - on Vo mean that you are to subtract the voltage on the negative end from the voltage from the positive end. It is that potential difference that the voltage dependent voltage source is tied to. Since with the given current direction there is a actually a voltage DROP from the minus end to the plus end (passive sign convention) that voltage difference is negative. Thus that voltage is - 6*i.

I see, thanks a lot.