- #1
chever
- 8
- 0
[Disclaimer: I'm pretty sure this doesn't belong in the HW questions forum. I'm a linguistics major not taking any EE courses and it's the summertime. I just happen to be using an undergrad EE text.]
For the life of me I cannot crack the following:
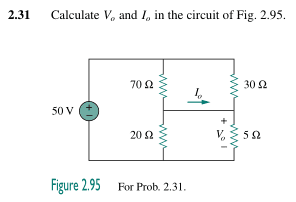
Since I believe the 70 and 30 ohm resistors are in parallel, likewise the 20 and 5 ohm resistors, I tried finding the total current through the circuit by combining them and then combining the two equivalent in series but I'm not even sure I can do that and I really am just stuck at this point.
Your help would be greatly appreciated.
For the life of me I cannot crack the following:
Since I believe the 70 and 30 ohm resistors are in parallel, likewise the 20 and 5 ohm resistors, I tried finding the total current through the circuit by combining them and then combining the two equivalent in series but I'm not even sure I can do that and I really am just stuck at this point.
Your help would be greatly appreciated.