TachyonLord
- 54
- 6
Homework Statement
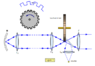
In the Fizeau's Experiment to determine the speed of light, let the gear have N teeth, the frequency of the rotating gear being f, the distance traveled by the light beam/ray L (distance b/w the gear and the mirror) and let there be n eclipses(blocking of the light beam).
Calculate the speed of light.
More information on the experiment :
Homework Equations
$$Speed =\frac {Distance} {Time}$$
$$ f = \frac 1 T$$
Angular frequency(w) = 2πf
The Attempt at a Solution
So I tried solving this by using $$c(speed of light) = \frac {2L} t$$
where T will be the time for the light to pass through the teeth and then be reflected.If T is the time period of the gear, then $$t = \frac T {2N}$$
because I'm thinking that the time for one eclipse should be the time taken to go from A to B, which is equivalent to one tooth's length.
$$⇒ t = \frac {1} {2fN}$$
And subsequently, c = 4LfN , but this doesn't include n.
So I tried a different approach and used the formula $$t = \frac d v$$
$$d = \frac {2πR} {2N}$$
v = (2πf)R
which again gives the same answer, without the n term.
I also thought of another situation, where the light goes through the gap and is blocked by some tooth(which is not the successive one) which seems absurd in itself and I don't really know how to continue.
The answer that was annouced in the class had something like (2n-1) in the denominator. I don't know where I'm going wrong.
Thank you.
Attachments
Last edited: