Flow Rate in Horizontal Rectangular Channel: Solve Now

[Ragnar1995]

Homework Statement

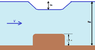
In a horizontal rectangular open channel 20 m wide the water depth is 9 m. When a
smooth hump 1.5 m high is introduced in the channel floor, a drop of 1 m is produced in
the water surface. What is the flow rate, neglecting energy losses? It is proposed to place
a pier at the centre of this channel on the hump. Determine the maximum width of this
pier if it is not to cause any backwater effects.
[/B]

Homework Equations

all the equations i can think of are :
E=h+(v^2/2g) also h+(v^2/2g)=constant
E=h+(q^2/2gh^2)
hc=(q^2/g)^1/3
Emin=1.5hc
Q=qB
E1=y+E2
v=q/h

Where E=specific energy
h=depth of flow
hc=critical depth
q=flow rate per unit width
Q=flow rate[/B]

The Attempt at a Solution

First of i tried to find velocities at each point using :

h+(v^2/2g)=constant

9+v1^2/2g = 6.5+v2^2/2g

and i got to v1-v2=7m/s, wasnt sure what to do from there, so i tried a different method...

I assumed the critical depth would be 6.5, Emin=1.5hc given Emin=9.75

I then subbed that into the equation E=h+(v^2/2g) to give v=7.99m/s

i then subbed into eq v=q/h to give q=51.935

then Q=qB
= 51.935 x 20
=1038.7 m^3/s

however answer is
832.52 m^3
/s
any help would be appreciated. Thanks




[/B]

 

[TSny]

I'm not sure I'm interpreting the problem correctly. I have attached a figure. I assume the hump goes across the entire width of the channel.

The Attempt at a Solution

First of i tried to find velocities at each point using :

h+(v^2/2g)=constant

9+v1^2/2g = 6.5+v2^2/2g

and i got to v1-v2=7m/s, wasnt sure what to do from there,
[/B]

When using the formula h + v²/(2g) = const. you have apparently chosen two points in the fluid flow to apply the equation. Can you describe the location of these two points? Where are you choosing h = 0? Have you measured the height h for the two points from the same reference level (h = 0)?

Also note that $\sqrt{v_2^2 - v_1^2} \neq v_2 - v_1$.

 

[haruspex]

9+v1^2/2g = 6.5+v2^2/2g

Think again about that 6.5m. Remember that this term represents the lost PE. How does the height of the bump come into that?