- #1
Kushwoho44
- 25
- 1
Homework Statement
The attempt at a solution
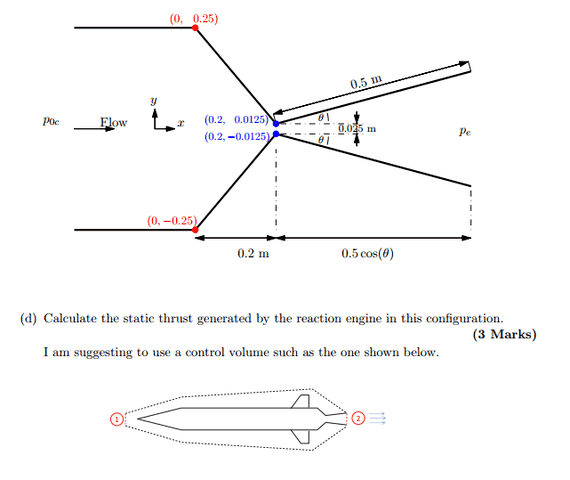
Hi all, I am tasked with finding the static thrust generated by this convergent-divergent nozzle. The stagnation pressure is known the inlet.
Now, personally, I would've thought drawn a control volume around the entire nozzle. And then said:
Net_Thurst = Pressure_inlet *A_inlet -Pressure_outlet*A_outlet.
Now, this does not yield the correct answer. I am not asking for the answer, rather, what is wrong with my understanding of the problem?
Thanks for the help!
The attempt at a solution
Hi all, I am tasked with finding the static thrust generated by this convergent-divergent nozzle. The stagnation pressure is known the inlet.
Now, personally, I would've thought drawn a control volume around the entire nozzle. And then said:
Net_Thurst = Pressure_inlet *A_inlet -Pressure_outlet*A_outlet.
Now, this does not yield the correct answer. I am not asking for the answer, rather, what is wrong with my understanding of the problem?
Thanks for the help!