Noorac
- 13
- 0
Hi, this is some questions about fluid dynamics(mostly). There are three somewhat connected questions here, I will try to organize it as best as I can.
A sylindrical tank filled with water is standing on a table, the tank has a small hole at the side of the tank at the very bottom(not underneath). The tank is placed on the table so that the water coming out of the hole will drop directly to the floor(it won't touch the table).
Variables:
Hight of table(hight from the hole in the tank to the ground) = H
Hight of waterlevel inside the tank = h
(inside)Radius of hole at the bottom of the tank = r
(inside)Radius of the tank = R
Speed at which the waterlevel inside the tank drops = V
Speed of the water flowing out of the hole = v
Distance on the floor, from the floor directly beneath the hole to where the water hits the floor = L.
I've added a sketch of the variables.
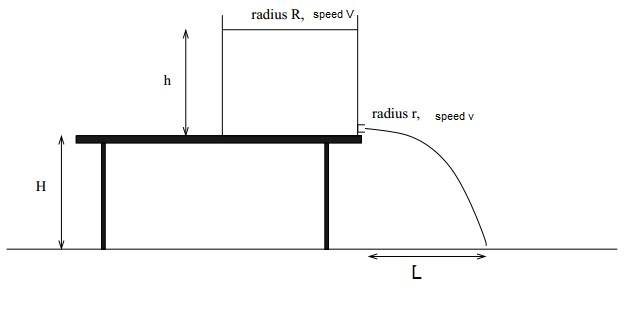
The airpressure is constant everywhere, g is gravity and works in the negative y direction, and the density of the water is constant.
Q1: What is the relation between the speed v and the speed V?
Q2: The speed V is related to the timedependancy of hight h by some differentiate. What is the relation?
Q3: What is the length L as a function of hight h?
- Bernoullis equation for incompressible liquid(see attempt at solution).
A1: The relation can be given by \rho t v \pi r^2 = \rho t V \pi R^2 = constant
Wich means vr^2 = VR^2 = constant. I don't know what more i need to do in order to show the relation, is this enough?
A2: I don't know how to solve this.
A3: I used Bernoullis equation to get a model for v: v = \sqrt{2gh}. So now I have the speed v out of the hole(i think), but don't know how to get from there. It is supposed to be a function of hight h, so I think I'm not supposed to mix time into it, in which case it would be easier.
I'm mostly interested in a small push in the right direction, and any help would be much appreciated=)
Edit: I forgot to say the mass is conserved!
Homework Statement
A sylindrical tank filled with water is standing on a table, the tank has a small hole at the side of the tank at the very bottom(not underneath). The tank is placed on the table so that the water coming out of the hole will drop directly to the floor(it won't touch the table).
Variables:
Hight of table(hight from the hole in the tank to the ground) = H
Hight of waterlevel inside the tank = h
(inside)Radius of hole at the bottom of the tank = r
(inside)Radius of the tank = R
Speed at which the waterlevel inside the tank drops = V
Speed of the water flowing out of the hole = v
Distance on the floor, from the floor directly beneath the hole to where the water hits the floor = L.
I've added a sketch of the variables.
The airpressure is constant everywhere, g is gravity and works in the negative y direction, and the density of the water is constant.
Q1: What is the relation between the speed v and the speed V?
Q2: The speed V is related to the timedependancy of hight h by some differentiate. What is the relation?
Q3: What is the length L as a function of hight h?
Homework Equations
- Bernoullis equation for incompressible liquid(see attempt at solution).
The Attempt at a Solution
A1: The relation can be given by \rho t v \pi r^2 = \rho t V \pi R^2 = constant
Wich means vr^2 = VR^2 = constant. I don't know what more i need to do in order to show the relation, is this enough?
A2: I don't know how to solve this.
A3: I used Bernoullis equation to get a model for v: v = \sqrt{2gh}. So now I have the speed v out of the hole(i think), but don't know how to get from there. It is supposed to be a function of hight h, so I think I'm not supposed to mix time into it, in which case it would be easier.
I'm mostly interested in a small push in the right direction, and any help would be much appreciated=)
Edit: I forgot to say the mass is conserved!
Last edited: