Flux through a cube at an angle

[nilesthebrave]

Homework Statement

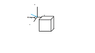
A uniform electric field with a magnitude of 600 N/C is shown pointing in the y-z plane, at 30 degrees from the +y axis and at 60 degrees from the +z axis. This electric field passes through a cube, with each side of length 2.0cm and oriented with faces in the +x, +y, and +z directions. For each face of the cube, calculate the electric flux, and then add these results to find the net electric flux.

Homework Equations

\Phi =EAcos \theta

The Attempt at a Solution

I started off doing the left face:
(600)(.02)^2cos60=0.12

What I'm not sure on, and I guess what I'm more questioning is, since the field is at this angle do I need to set the equation up differently? My instructor has never shown us any problem like this, nor is there one in my book. Everything is always parallel or perpendicular in the examples, so do I do anything different here?

 

[nilesthebrave]

forgot to upload diagram

 

[nilesthebrave]

Disregard this, I was making it more difficult than it was. Problem solved.