issacnewton
- 1,035
- 37
Homework Statement
Homework Equations
Impulse momentum theorem, Newton's second law
The Attempt at a Solution
Now the water will impart some impulse to her. Let ##\bar{v_1}## be the initial horizontal velocity of the water jet and let ##\bar{v_2}## be the final vertical velocity of the jet. Then the force exerted by the woman on the jet would be
$$ \bar{F} = r\left( \bar{v_2} - \bar{v_1} \right) $$
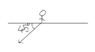
where ##r = 1.2\;kg/s## is the mass rate at which the jet is hitting her. Since ##\bar{v_1}## and ##\bar{v_2}## have the same magnitude of ##6\;m/s##, we can use the Pythagoras theorem to calculate ## bar{v_2} - \bar{v_1}## and hence ## \bar{F}##. Due to Newton's third law, the force exerted by the water jet on the woman will be exactly opposite in direction. So it turns out that this force will be directed at 45 degrees below horizontal as shown below. So horizontal component of
this force will be ## F\cos(45)##. Using the value of ##F##, this is
$$ F\cos(45) = 1.2\times 6\sqrt{2}\times \frac{1}{\sqrt{2}} = 7.2 N $$
and then using the Newton's second law for the woman, her initial acceleration would be
$$ a = F/m = \frac{7.2}{50} = 0.144\; m/s^2 $$
Is this correct so far ? For part b, I am confused. If there is a constant force impacted by the water jet, then why would the speed of the woman increase only till some maximum value ?