Doc Al said:
Maybe I'm missing something (besides a few marbles), but why not treat this as a straightforward dynamics problem?
From Newton's 2nd law:
mg - N = ma
N (L/2) \sin A = I \alpha
The rotational inertia about the cm is:
I = 1/12 m L^2
The constraint of the contact point slipping along the floor gives:
a = \alpha (L/2)\sin A
Solving the above, I get:
N = mg/(1 + 3\sin^2 A)
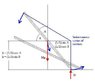
I think I have finally caught up to you and siddharth on this thing. You are right of course about the conservation of energy. I guess I had a serious brain burp, or a senior moment on that one. siddharth was right all along on the velocity issue, though it took me to his latest discription to get in touch with his instantaneous center of rotation notion. A picture is helpful in this regard, so I drew one up and am posting it here. Please check it siddharth and make sure I have interpreted it correctly. The diagram does seem to fit with the case you were making and the final result.
I did manage to work through the energy approach and got the same result once I fixed the velocity to angular velocity relationship. It does not add anything to what has already been done, except that in the course of doing it I believe I have extended the problem to the case of what happens to the normal force after the rod is in motion. It is not a closed form solution because there is a term that depends on the angular (or linear if you want to put it in those terms) velocity. It is posted here from the F = ma and \tau = I\alpha point of view that you followed, and includes the calculation of the relationship between a and \alpha that leads to the velocity dependence of the normal force.
Newton's second law
h = \frac{L}{2}\cos A
\frac{{dh}}{{dt}} = - \frac{L}{2}\omega \sin A = v
\frac{{d^2 h}}{{dt^2 }} = - \frac{L}{2}\left( {\alpha \sin A + \omega ^2 \cos A} \right) = a
N - mg = ma = - m\frac{L}{2}\left( {\alpha \sin A + \omega ^2 \cos A} \right)
N - mg = - \frac{{mL\alpha }}{2}\sin A - \frac{{mL\omega ^2 }}{2}\cos A
Torque
N\frac{L}{2}\sin A = I\alpha {\rm{ ; }}I = \frac{{mL^2 }}{{12}}
<br />
\frac{{N\sin A}}{2} = \frac{{I\alpha }}{L} = \frac{{mL\alpha }}{{12}} = \frac{1}{6}\frac{{mL\alpha }}{2}
\frac{{mL\alpha }}{2} = 3N\sin A
Substituting
N - mg = - \frac{{mL\alpha }}{2}\sin A - \frac{{mL\omega ^2 }}{2}\cos A
N = mg - 3N\sin ^2 A - \frac{{mL\omega ^2 }}{2}\cos A
N\left( {1 + 3\sin ^2 A} \right) = mg - \frac{{mL\omega ^2 }}{2}\cos A
N = \frac{{2mg - mL\omega ^2 \cos A}}{{2 + 6\sin ^2 A}}
For the stated condition that the Normal force at the time of release is to be found, this result reduces to your result because at that moment \omega is zero.
I think an interpretation of this result is that if you started with an initial \omega you might get to a point where the rotation creates separation from the floor before the rod hits flat. I'm wondering if it might happen even if you release the rod from rest. I dropped a pencil a few times, and it looks to me like there might be separation before it hits, but it is hard to tell. Someone else might want to explore that and get a closed form solution, but I'm done with this one for a while.