Force/Magnetism direction question (w/diagram)

[nophun6]

I have a question regarding electrical charge, magnetic field, and force.
Given this diagram, and assuming a positive electrical charge, I have to show:
Fig 1: direction of the force
Fig 2: direction of the force
Fig 3: direction of the velocity
Fig 4: direction of the magnetic field

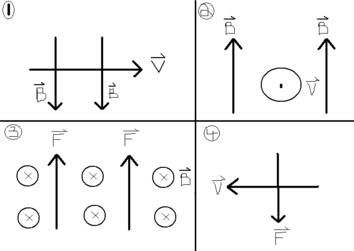
*Figure 2, the circle with the dot means that the vector is coming out of the plane of the page
*Figure 3, the circle with the X means that the vector is going into the plane of the page

I have the understanding that the direction of the Force, F, acting on an electric charge is perpendicular to both the directions of the magnetic field, B, and the velocity, V. Is this assumption correct, and also what effect does it have on the direction of the force, magnetic field and velocity if the electrical charge is switched from positive to negative? I would imagine that velocity wouldn't change and the magnetic field would reverse. is this right?

 

[xman]

From Lorentz law
\vec{F} = q \left( \vec{E} + \vec{v} \wedge \vec{B} \right)
so if the electric field is zero, then
\vec{F} = q \vec{v} \wedge \vec{B}
so use the RHR and you should be able to tell what direction the force is in. Now if we replace the test charge, from q to -q, then by convention, the force acts opposite the direction as on the positive charge. hope this helps, x

 

[nophun6]

i don't know how to apply that equation in order to get the direction. i tried using the right hand rule, and just can't figure it out for the 1, 2, and 3, but i think i got 4, haha. I think the direction of the magnetic field would be pointing up and to the left, starting at the intersection of the F and V lines

 

[mezarashi]

The right hand rule works wonders if you properly understand how to use it. Shape your hand like a gun. Let your index finger be the direction of moving charge (positive charge). Let the rest of your three fingers be the magnetic field lines. Your thumb now indicates the direction of the induced force.

Don't be shy to have to move around to align your hand with the screen or even twist your hand or arms around so that the said directions look aligned with your fingers. You should have seen the scene in the exam hall during my high school electricity & magnetism exam ^_^;;. There's a learning curve, but sooner or later you'll even be able to do it in your head.

 

[nophun6]

Thanks for the help, i retried the rhr and got these answer. Can someone please verify if they are rihgt. thanks.

For Figure 1: The direction of the force is going into the plane of the page.

For Figure 2, using the rhr, i get the direction of the force pointing to the left. Is this correct? and if so would I just draw an arrow pointing to the left and write F next to it?

For Figure 3: I got that the direction the moving charge, V, would be pointing right.

Figure 4: the magnetic field, B, is pointing into the plane of the page.

 

[Roze]

I agree with the answers you provided, but I am still new to the right hand rule so you probably want a better authority on it.

How would this change if the charge was a negative one? In parts a and b I know the force would be opposite, but for c and d we are given the force in a direction, so how does our answer change with a negative charge?

Thanks!