blondii
- 31
- 0
Homework Statement
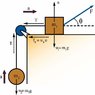
A block of mass m1 on a rough horizontal surface is connected to a ball of mass m2 by a light weight cord over a light weight, friction-less pulley, as shown in the figure below. A force of magnitude F at an angle θ with the horizontal is applied to the block as shown. The coefficient of kinetic friction between the block and surface is uk. Determine the magnitude of the acceleration of the two objects.
Homework Equations
Refer to attachment
The Attempt at a Solution
I would just like to confirm my answer. Better still if anyone can suggest a shorter way of solving it would be nice. Please find my complete solutions on pdf attached. Thanks