Becca93
- 84
- 1
Homework Statement
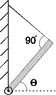
A 26.6 kg beam is attached to a wall with a hinge and its far end is supported by a cable. The angle between the beam and the cable is 90°. If the beam is inclined at an angle of theta=13.3° with respect to horizontal, what is the horizontal component of the force exerted by the hinge on the beam? (Use the 'to the right' as + for the horizontal direction.)
Hint: The Net torque and the Net Force on the hinge must be zero since it is in equilibrium.
What is the magnitude of the force that the beam exerts on the hinge?
(Image attached)
I already knew that the net force and net torque would be zero, so I set clockwise and counter clockwise torque equal to each other
τcw = τccw
Fdsinθ = Fdsinθ
And this is where I ran into trouble. Length of the beam is never given. I'm not really sure what angles to use where, and while I know that the force the beam exerts on the wall/hinge is equal and opposite to what the wall/hinge exerts on the beam, I'm not sure how to find it.
To find the magnitude of force in the second half of the problem, you would just take magnitude = √(Fx^2 + Fy^2), correct?
Any advice?
A 26.6 kg beam is attached to a wall with a hinge and its far end is supported by a cable. The angle between the beam and the cable is 90°. If the beam is inclined at an angle of theta=13.3° with respect to horizontal, what is the horizontal component of the force exerted by the hinge on the beam? (Use the 'to the right' as + for the horizontal direction.)
Hint: The Net torque and the Net Force on the hinge must be zero since it is in equilibrium.
What is the magnitude of the force that the beam exerts on the hinge?
(Image attached)
The Attempt at a Solution
I already knew that the net force and net torque would be zero, so I set clockwise and counter clockwise torque equal to each other
τcw = τccw
Fdsinθ = Fdsinθ
And this is where I ran into trouble. Length of the beam is never given. I'm not really sure what angles to use where, and while I know that the force the beam exerts on the wall/hinge is equal and opposite to what the wall/hinge exerts on the beam, I'm not sure how to find it.
To find the magnitude of force in the second half of the problem, you would just take magnitude = √(Fx^2 + Fy^2), correct?
Any advice?