SUMMARY
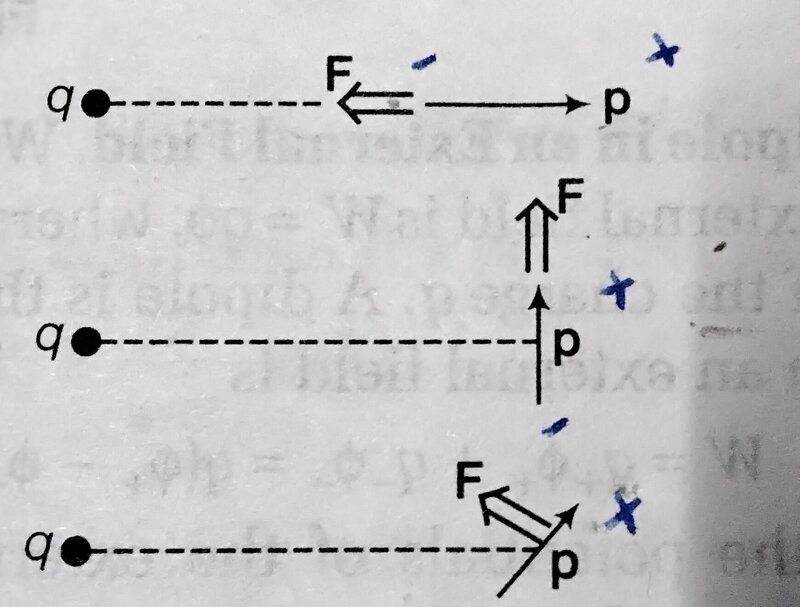
The discussion centers on the calculation of force on an electric dipole in a non-uniform electric field, specifically referencing the equation F = p * (∂E/∂x, ∂E/∂y, ∂E/∂z). Participants clarify that the partial derivative should be taken with respect to spatial coordinates rather than the direction of the dipole moment vector (p). The conversation highlights the importance of understanding the configuration of the dipole and the electric field, as well as the necessity of showing work for accurate assistance. Ultimately, the original poster acknowledges a misinterpretation of the problem statement.
PREREQUISITES
- Understanding of electric dipoles and their behavior in electric fields
- Familiarity with vector calculus, specifically partial derivatives
- Knowledge of Newton's laws of motion as they apply to forces
- Ability to interpret and analyze diagrams related to electric fields
NEXT STEPS
- Study the derivation of the force on a dipole in a non-uniform electric field using F = p * (∂E/∂x, ∂E/∂y, ∂E/∂z)
- Learn about different coordinate systems and their applications in vector calculus
- Explore the concept of torque in relation to forces acting on dipoles
- Review examples of electric dipoles in various configurations to solidify understanding
USEFUL FOR
Students and educators in physics, particularly those studying electromagnetism, as well as anyone involved in solving problems related to electric dipoles and non-uniform electric fields.