- #1
kapital
- 19
- 0
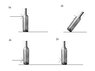
If we act with force on bottle in two different way, we get two results:
a) If push(with hand) bottle at upper side of it, it will fall down(go to horizontal position),but if we
b) push bottle with the same force at lower side, it will move forward.
Why is this happening? Could we calculate at which height is limit from where one occurrence come to other?
a) If push(with hand) bottle at upper side of it, it will fall down(go to horizontal position),but if we
b) push bottle with the same force at lower side, it will move forward.
Why is this happening? Could we calculate at which height is limit from where one occurrence come to other?