Forced Oscillations: Pendulum 1 Driving Neighboring Pendulum

[Kaushik]

TL;DR Summary

.

Consider the following setup:

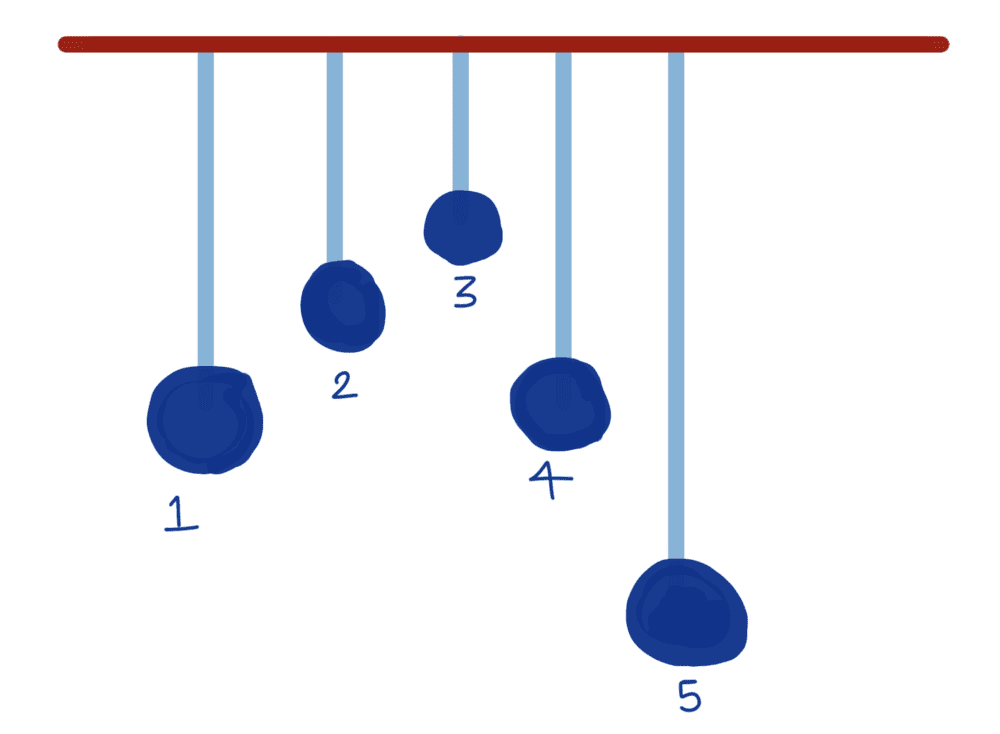
In this, let us set the pendulum 1 into motion. The energy gets transferred through the connecting rod and the other pendulum starts oscillating due to the driving force provided by the oscillating pendulum 1. Isn't it?
So the neighbouring pendulum starts oscillating with their natural frequency at first but as time passes, the natural frequency die out due to dissipative forces. Then once the natural frequency dies out, they start oscillating with the frequency of pendulum 1.
So I don't understand how the pendulum starts oscillating with 'natural frequency' even though the cause for oscillation is the external force due to pendulum 1. This is probably because of my misinterpretation of natural frequency.

 

[etotheipi]

The natural frequency of oscillation of any given pendulum depends on only its length (and g). The driver will be significantly more massive than the other pendula.

If we set the driver in motion, it has the effect of applying a driving force to each of the other pendula (via the connecting rod). It is possible to derive the steady state phase difference between force and displacement for a damped driven oscillator; do you know what the phase difference is in the cases when the forcing frequency is less than, equal to or greater than the natural frequency, considering each of the pendula 2, 3, 4 and 5 in turn?

 

[sophiecentaur]

Summary:: .

This is probably because of my misinterpretation of natural frequency.

Natural frequency is the frequency of oscillation in total isolation from other forces. You can force oscillations at other frequencies and the amplitude of the oscillation will depend on the natural frequency and the Q factor. The Q ('Quality') factor is a function of dissipative forces and will be higher as the friction etc gets less. Q represents the rate at which energy builds up or dissipates in a resonant system. The multiple pendula in your OP are 'coupled' to each other by the top string. Ignore any friction / damping and the energy will constantly couple from one to another so that their amplitudes build up and decay. The frequencies of their oscillations will be near but not equal to their individual natural frequencies because they are 'forced' oscillations. The experiment works best when the differences in natural frequencies is not too great and when the Q factors are very high. Best to consider only two pendula first.