drkidd22
- 59
- 0
Homework Statement
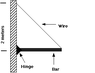
In the figure below, the bar is 3.4 meters long and has a mass of 100 kg.
what is the magnitude of the hinge force?
The Attempt at a Solution
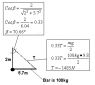
cosβ=2/sqrt(2^2+3.4^2)
cosβ=0.51
0.51T=mg/2
T= 100*9.8/(2*0.51)=960.8
I'm not 100% sure if I did this right.
Any assistance will be appreciated.