IgorT75
- 4
- 2
Summary:: What is the force N which acts on a support point at the moment just after system is released?
[Thread moved from the technical forums, so no Homework Template is shown]
A light bar with m1 and m2 masses (m1≠m2) at the ends placed on the support point (in the middle of the bar).
Initially it is held in this position (by hands let's say). Then it's released.
What is the force N which acts on a support point at the moment just after system is released?
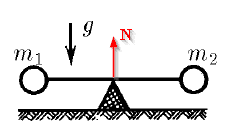
[Thread moved from the technical forums, so no Homework Template is shown]
A light bar with m1 and m2 masses (m1≠m2) at the ends placed on the support point (in the middle of the bar).
Initially it is held in this position (by hands let's say). Then it's released.
What is the force N which acts on a support point at the moment just after system is released?
Last edited by a moderator: