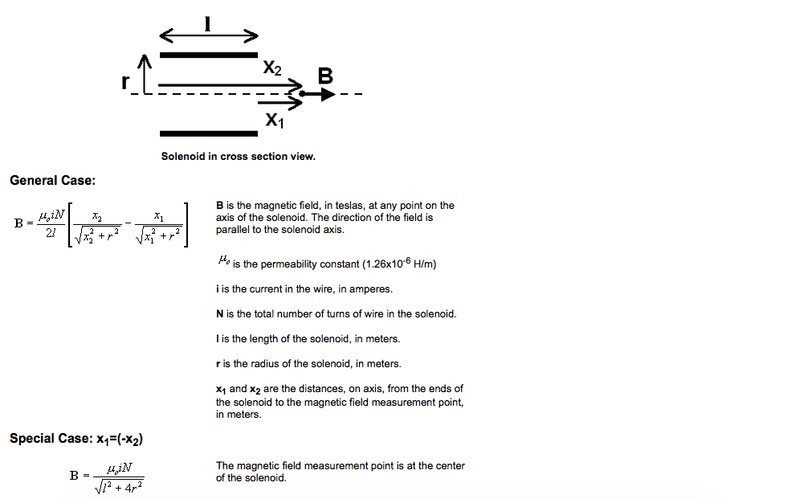
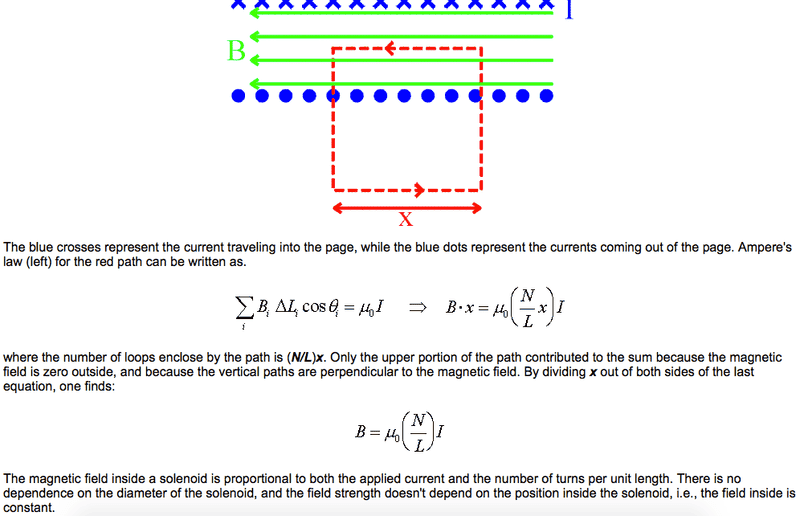
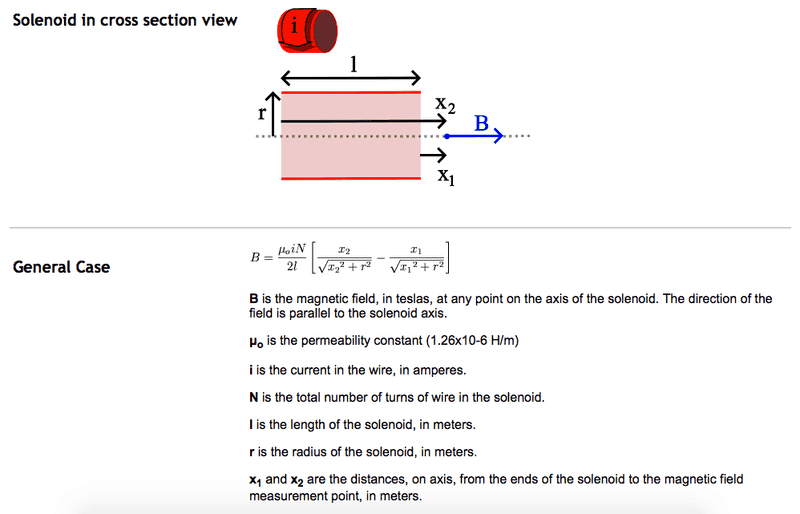
First of all you draw a circulation path like the one in photo #4, just wider ( larger x ) so that the path crosses the point P.
Using Amperes law you can easily calculate the mean value of H: H
mean1 = ( N * I ) / s , s is the length of the path.
Biot-Savart says, as for vacuum (
boldface means vector ):
d
B = ( μ
0 * i
ds x
r ) / ( 4π*r
3 ) →
d
H = ( i
ds x
r ) / ( 4π*r
3 )
Of course you should be able to find H
mean1 again by integration of (
H(s)⋅ds ) / s along the
exactly same path in vacuum.
Now you insert electric steel ( μ
r = 4000 ) as core in the solenoid, and the H-field will be disorganized. Anyway just integrate through the path, but when you pass through the steel, you divide
H(s) by μ
r. Call the result of the integration H
mean2.
Of course you will find that H
mean2 ≠ H
mean1. Say that H
mean2 = k * H
mean1 , ( k will be less than 1 ).
But you can make H
mean1 = H
mean2 by dividing
all the
H(s) ( found by Biot-Savart ) by k. Of special interest is of course
H(P).
I think that will work. What do you think ?

PS: You should use numeric integration. Say you divide the the coil into 84000
ds's ( 1000
ds's per turn ) and the magnetic path into 10000
ds's, the computer will have to calculate Biot-Savart 840E6 times. Say that each calcultion is done in 10 μs, the computer will do the job in about 2½ hour. So set Amperes (i) = 1, and so on. You can always multiply the result by 5 afterwards. Don't use excel, it will never end.